We have a vector field $\mathbf{F} = 0.4 (-\mathbf{i}-\mathbf{j}+\mathbf{k})$ and want to calculate the flux through a window which consists of joining, in turn, the following points with straight line segments: $(1,1,0),(1,0,0),(0,0,0),(0,1,1),(1,1,1),(1,1,0)$
Which gives a weird looking wedge shape pictured below:
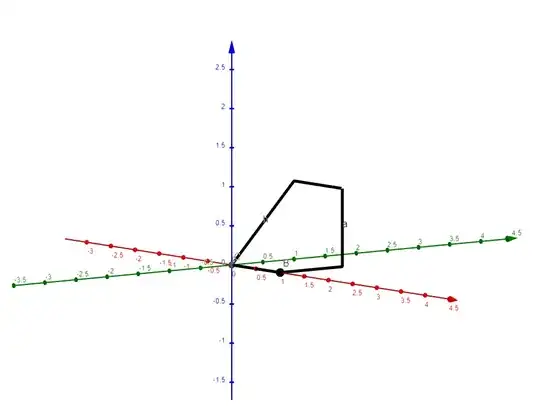
Since this loop does not have an easily definable normal vector which we can use to find the flux using $\int_S \mathbf{F} \cdot \mathbf{dS} = \int_S \mathbf{F} \cdot \mathbf{\hat n}\,dS$, I was unsure how to proceed. I know we basically want to find the cross section from the vector fields point of view, so to speak, and when viewing the loop along the direction of the force, we see:
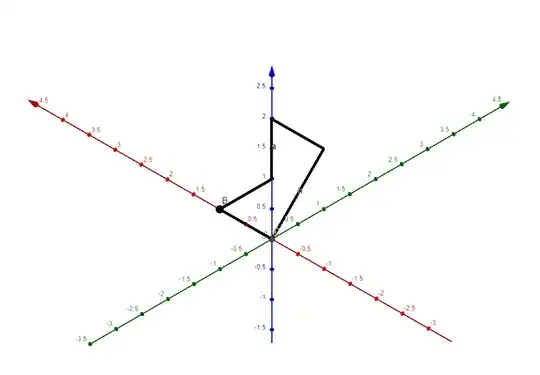
And I could find this cross section from here, but am looking for a method that doesn't involve looking at the physical cross section and summing triangle areas. Is there a way to do this "normally" (without heavily relying on geometry)?