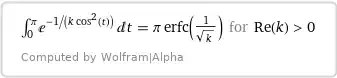Are there methods to analytically compute this integral, composed of the maximum function, $max(\exp(x_{0})-\exp(z_{0}), 0)$, and exponential functions?
$$\iint_{-\infty}^{\infty}\tilde{A}\max(\exp(x_{0})-\exp(z_{0}), 0)\exp(A_{2}(x_{M}-x_{0})^2)\exp(2A_{2}\alpha_{1}(x_{M}-x_{0}))\exp(-2A_{2}\Omega(x_{M}-x_{0}+\alpha_{1})(z_{M}-z_{0}))\exp(A_{2}\Omega^2(z_{M}-z_{0})^{2})\exp(A_{5}(z_{M}-z_{0}))\exp(A_{6}(z_{M}-z_{0})^{2})dx_{0}dz_{0}$$
$\tilde{A},A_{2},\alpha_{1},\Omega,A_{5},A_{6},x_{M},z_{M}$ are constants. Specifically, $\tilde{A},A_{2},A_{5},A_{6}$ are negative, while the others take on any real number.
So now let $x_{M}-x_{0}= {x}'$ and $z_{M}-z_{0}= {z}'$.
We transform the integral to:
$$\iint_{\infty}^{-\infty}\tilde{A}\max(\exp(x_{M}-{x}')-\exp(z_{M}-{z}'), 0)\exp(A_{2}({x}')^2)\exp(2A_{2}\alpha_{1}({x}'))\exp(-2A_{2}\Omega({x}')({z}'))\exp(A_{2}\Omega^2({z}')^{2})\exp((A_{5}-2A_{2}\Omega\alpha_{1})({z}'))\exp(A_{6}({z}')^{2})d{x}'d{z}'$$
where the limits have changed because of the substitution.
The exponent can now elegantly be written as:
$$\left ( {x}', {z}' \right )\begin{pmatrix} A_{2} & -A_{2}\Omega \\ -A_{2}\Omega & A_{6}+A_{2}\Omega^2 \end{pmatrix}\left ( {x}', {z}' \right )^{T} +\left ( 2A_{2}\alpha_{1},(A_{5}-2A_{2}\Omega\alpha_{1}) \right )\left ( {x}', {z}' \right )^{T}$$
and by letting $ \hat{A}=\begin{pmatrix} A_{2} & -A_{2}\Omega \\ -A_{2}\Omega & A_{6}+A_{2}\Omega^2 \end{pmatrix}$ and $ J=\left ( 2A_{2}\alpha_{1},(A_{5}-2A_{2}\Omega\alpha_{1})\right )$
The integral becomes $$\iint_{\infty}^{-\infty}\tilde{A}\max(\exp(x_{M}-{x}')-\exp(z_{M}-{z}'), 0)\exp(\left ( {x}', {z}' \right )\hat{A}\left ( {x}', {z}' \right )^{T}+J\left ( {x}', {z}' \right )^{T})d{x}'d{z}'$$
I have tried doing a simpler integral:
$\iint_{-\infty}^{\infty}\tilde{A}\max(\exp(x_{0})-\exp(z_{0}), 0)\exp(A_{1}(x_{M}-x_{0}-\alpha_{1})^2)\exp(A_{6}(z_{M}-z_{0}-\alpha_{2})^{2})dx_{0}dz_{0}$
but still can not reach a closed-form solution involving error function, dilogarithms, etc ...