2

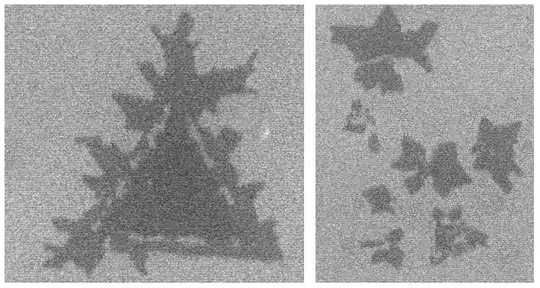
I am doing a dissertation in Materials Engineering. I obtained the following images regarding crystal growth:

enter image description here

In the literature they usually call these structures "fractals" and calculate their fractal dimension using the box-counting method. From what I read on the internet, a fractal has to have self-similarity.

However, these structures appear to be so irregular that they do not appear to have any kind of repetition. The fractals according to the DLA (diffusion limited aggregation) have a fractal dimension of approximately 1.70, which is close to that of these structures. Why do the authors consider these structures fractal if there is no self-similarity? What are the characteristics necessary for a figure to be considered a fractal?

Carmen González
  • 195
  • 2
    No. We often form fractals by iterative processes that produce self-similarity, but this is just because that is the easiest way to do so. And the results are often very interesting. But that is not what defines "fractal". As is often the case, 3Blue1Brown has a nice video about it. – Paul Sinclair Feb 12 '21 at 00:04
  • @PaulSinclair Thank you! Your comment was so simple that it was very informative. This was the idea he needed: that the condition of self-similarity is imposed on the system. Thanks for the explanation. – Carmen González Feb 12 '21 at 12:29

1 Answers1

2

This is more a comment than an answer, but I don't have the reputation.

Just a guess: A way that fractals arise is by iteration of a map. Perhaps what the authors have in mind is that the growth of these structures comes about by iteration of some simple rules, after translation or some simple function perhaps? The reason I'm saying this is that as far as I know, this sense of fractal (really just an approximate fractal) is what I would expect to see in nature, more than bona fide fractals.

Fox Mulder
  • 171
  • I think that they really referred to the concept of fratal itself, because the DLA model is associated with fractal growth. I don't understand if a fractal necessarily has to be self-similar. Do you know if that is a necessary and sufficient condition? – Carmen González Feb 11 '21 at 17:30
  • 1
    I recall one book that defined a fractal as a subspace of $\Bbb R^n$ (for some $n\in\Bbb Z^+$) whose Hausdorff-Besicovitch dimension in $\Bbb R^n$ is greater than its Small Inductive dimension. Apparently there are varying def'ns in use. – DanielWainfleet Feb 11 '21 at 23:09