Mapping from a perspective projected square to the original one

Question

A square viewed from an angle becomes an isosceles trapezoid. Assuming we are looking at the middle of the square, if we know everything about this trapezoid, how to map every coordinate on it to the original square?

The intersection of the trapezoid's diagonals is the midpoint of the square. From there, we can calculate the width (and thus height) of the square, by finding the width of the trapezoid at the y coordinate of the midpoint.
It seems to me that this allows us to find the corresponding x coordinate on the square for any point on the trapezoid by linearly interpolating the width.

A more complicated matter, and the subject of this question is finding the y coordinate on the square. For simplicity, let us assume that the top of the trapezoid is at y = 0, and the bottom is at y = 1. Same for the square.
Obviously the top of the trapezoid maps to the top of the square, and the bottom to the bottom. So 0 maps to 0, and 1 maps to 1. Again using the midpoint of the square which we located on the trapezoid by its diagonals, we can find that 1/(p+1) maps to 0.5, where p is the ratio between the bottom and top base lengths.
Visually, it is evident that we can continue finding the midpoints between any two found points, effectively allowing us to find any point, and showing that the mapping I seek exists, but aside from a complicated recursive definition, I can't find a formula for it. Any ideas?

Answer 1

TL;DR: See $\eqref{G4}$ below, under "There is a single solution, yielding".

Without loss of generality, we can pick a 3D coordinate system where the eye is at origin $(0, 0, 0)$, we look along the positive $z$ axis, $x$ axis being right, $y$ axis up, and the projective plane is at $z = 1$; and we have a rectangle with vertices at $(-x_r, y_0, z_0)$, $(x_r, y_0, z_0)$, $(x_r, y_1, z_1)$, and $(-x_r, y_1, z_1)$. Perspective projection to the projective plane at $z = 1$ is $$\left\lbrace \, \begin{aligned} \chi = x^\prime &= \frac{x}{z} \\ \gamma = y^\prime &= \frac{y}{z} \\ z^\prime &= \frac{z}{z} = 1 \\ \end{aligned} \right.$$ Note, this is not an approximation, this is exact with the above conditions.

The projected coordinates for the four vertices are $$\left\lbrace \, \begin{aligned} \chi_{00} &= -\frac{x_r}{z_0} \\ \gamma_{00} &= \frac{y_0}{z_0} \\ \end{aligned} \right., \quad \left\lbrace \, \begin{aligned} \chi_{01} &= \frac{x_r}{z_0} \\ \gamma_{01} &= \frac{y_0}{z_0} \\ \end{aligned} \right., \quad \left\lbrace \, \begin{aligned} \chi_{10} &= -\frac{x_r}{z_1} \\ \gamma_{10} &= \frac{y_1}{z_1} \\ \end{aligned} \right., \quad \left\lbrace \, \begin{aligned} \chi_{11} &= \frac{x_r}{z_1} \\ \gamma_{11} &= \frac{y_1}{z_1} \\ \end{aligned} \right.$$

We can parametrise the surface of the rectangle with $0 \le u \le 1$, $0 \le v \le 1$ using $$\left\lbrace \, \begin{aligned} x &= x_r (2 u - 1) \\ y &= y_0 + (y_1 - y_0) v \\ z &= z_0 + (z_1 - z_0) v \\ \end{aligned} \right.$$ The projected coordinates for the parametrised surface are $$\left\lbrace \, \begin{aligned} \chi &= \frac{ x_r (2 u - 1) }{ z_0 + (z_1 - z_0) v } \\ \gamma &= \frac{ y_0 + (y_1 - y_0) u }{ z_0 + (z_1 - z_0) v } \\ \end{aligned} \right. \tag{1}\label{G1}$$ and its inverse is $$\left\lbrace \, \begin{aligned} u &= \frac{ \chi (y_0 z_1 - y_1 z_0) + \gamma x_r (z_1 - z_0) - x_r*(y_1 - y_0) }{ 2 \bigl ( \gamma x_r (z_1 - z_0) + x_r (y_0 - y_1) \bigr) } \\ v &= \frac{y_0 - \gamma z_0 }{ \gamma (z_1 - z_0) - (y_1 - y_0) } \\ \end{aligned} \right. \tag{2}\label{G2}$$ The last equation is the one we need, except that we also need a way to derive the constants $x_r$, $y_0$, $z_0$, $y_1$, and $z_1$ from the projected coordinates $\chi_{00}$ through $\gamma_{11}$.

However, now that we have the form of $u(\chi, \gamma)$ and $v(\chi, \gamma)$ functions, we can instead use that form with simple constants, and fit those constants to the observed coordinates!

(This is a trick I personally use often with Computer Algebra Systems like wxMaxima, because it is much less work than finding how to map the known constants to $\eqref{G2}$. As long as we don't accidentally omit any coefficients, this works perfectly. So, do compare $\eqref{G2}$ and $\eqref{G3}$ to see they have the same form.)

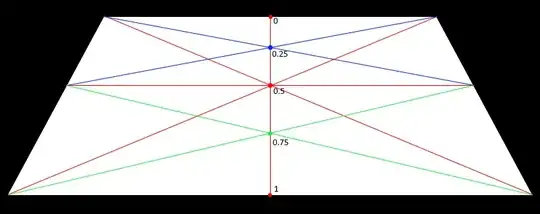
For simplicity, I will use $x$ (instead of $\chi$) for the projected $x$ coordinate, and $y$ (instead of $\gamma$) for the projected $y$ coordinate, since we no longer care about the actual 3D coordinates. We have $$\left\lbrace \, \begin{aligned} u(x, y) &= \frac{U_0 + U_1 x + U_2 y}{y + U_3} \\ v(x, y) &= \frac{V_0 + V_1 y}{y + V_2} \\ \end{aligned} \right. \tag{3}\label{G3}$$ Let's say the four vertices of the isosceles trapezoid are at $(-x_1, y_1)$, $(+x_1, y_1)$, $(+x_2, y_2)$, and $(-x_2, y_2)$. The diagonals cross at $(0, y_0)$, where $$y_0 = \frac{x_1 y_2 + x_2 y_1}{x_1 + x_2}$$ Now we have seven equations for seven unknowns to solve: $$\left\lbrace \, \begin{aligned} u(-x_1, y_1) &= 0 \\ u(+x_1, y_1) &= 1 \\ u(-x_1, y_2) &= 0 \\ u(+x_1, y_2) &= 1 \\ \end{aligned} \right. \quad \text{ and } \quad \left\lbrace \, \begin{aligned} v(0, y_1) &= 0 \\ v(0, y_0) &= \frac{1}{2} \\ v(0, y_2) &= 1 \\ \end{aligned} \right.$$ There is a single solution, yielding $$\left\lbrace \, \begin{aligned} u(x, y) &= \frac{ x (y_2 - y_1) + y (x_2 - x_1) + x_1 y_2 - x_2 y_1 }{2 \bigl( y (x_2 - x_1) + x_1 y_2 - x_2 y_1 \bigr) } \\ v(x,y) &= \frac{ (y - y_1) x_2 }{ y (x_2 - x_1) + x_1 y_2 - x_2 y_1 } \\ \end{aligned} \right. \tag{4}\label{G4}$$ Note that this is not an approximation; this is correct for any rectangle whose projected corners are at $(-x_1, y_1)$, $(+x_1, y_1)$, $(+x_2, y_2)$, and $(-x_2, y_2)$.

Also note that $u(-x_1, y_1) = u(-x_2, y_2) = 0$, $u(0, y) = 1/2$, $u(x_1, y_1) = u(x_2, y_2) = 1$, $v(x, y_1) = 0$, $v(x, y_2) = 1$, and $v(x, y_0) = 1/2$ where $y_0$ is the $y$ coordinate where the diagonals of the projected trapezoid intersect, $y_0 = (x_1 y_2 + x_2 y_1) / (x_1 + x_2)$.