Argument by symmetry that $\sum_{k=0}^{n-1} e^{2\pi i\frac{k}{n}}=0$

Question

By summing up the geometric series, it can be shown that,

$$\sum_{k=0}^{n-1} e^{2\pi i\frac{k}{n}}=\frac{1- e^{2\pi i\frac{n}{n}}}{1- e^{2\pi i\frac{1}{n}}}=0.$$

However despite having proof of this fact, it feels somewhat magical that the (signed) heights and widths of the right triangles formed by equally partitioning the unit circle always sum to zero.

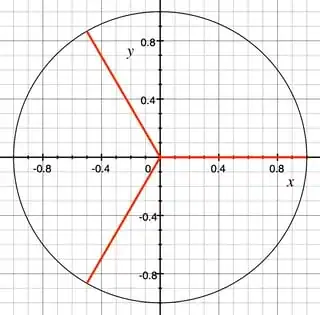
Consider the case with $n=3$, then we have

It's fairly easy to see in both this example, and in the general case, that the imaginary part always cancels by complex conjugate symmetry.

However even in the case of $n=3$, one does not have pairwise cancellation of the real part. Instead the right triangle widths corresponding to the two non-zero angles together are required to cancel out the third angle's corresponding width, i.e.

$$\cos\frac{2\pi}{3}+\cos\frac{4\pi}{3}=-1,$$

which to me is an entirely non-obvious fact.

So I'm wondering if there exists some argument by symmetry, from which one can deduce that $\sum_{k=0}^{n-1} e^{2\pi i\frac{k}{n}}=0$.

Answer 1

Let $S = \sum_{k=0}^{n-1} z^k$, where $z = e^{2\pi i/n}$. You want an argument by symmetry that $S = 0$. Note that $S$ is not $0$ when $n = 1$, so any argument offered has to distinguish $n = 1$ from $n > 1$.

The number $S$ is a sum over all solutions in $\mathbf C$ to $x^n = 1$, and for $n > 1$ the sum $S$ is symmetric in the roles of all of those solutions. Those solutions are symmetrically placed with respect to the origin and nowhere else, so wouldn't it be strange for $S$ to be located anywhere except $0$? This is not a serious proof, but an intuitive argument that it's reasonable to expect $S = 0$.

Here is a geometric argument by symmetry: the number $S/n$ is the average of the solutions of $x^n = 1$, the "center of mass" of those points. The solutions of $x^n = 1$ divide up the unit circle into $n$ equal arcs, and for $n > 1$ it is visually evident that their average is the center of the circle, which is $0$. Thus $S/n = 0$, so $S = 0$.

Here is an algebraic argument by symmetry: let $r$ be a solution of $r^n = 1$ with $r \not= 1$. Then $rS = \sum_{w^n = 1} rw = \sum_{w^n = 1} w = S$, where the second equation is due to multiplication by $r$ being a permutation of the solutions of $x^n = 1$. Since $rS = S$ and $r \not= 1$, $S = 0$. This algebraic argument is very important, because it is how a massive generalization of this result, called the orthogonality relation for characters, is proved in more advanced math.

Answer 2

A mechanical view (not an answer)

The equality

$$\sum_{k=0}^{n-1} e^{2\pi i\frac{k}{n}}=0$$ is asserting that the center of mass of a regular polygon is the center of the inscribed circle.

A way to "see it" is by deforming each edge of the polygon to the corresponding arc and to notice that the center of mass of a circle is located at its center.

Answer 3

Yes, you can prove that by geomery. I remember this method when I was a high school student.

Let's denote $A_1, A_2,...,A_n$ be the vertex of a regular n-polygon on the unit circle.

We have $S$ the sum of vectors, defined by $S = \sum_{i=1}^n \vec{OA_i}$ is equal to $\vec{0}$.

In deed, suppose by absurdity that the sum $S$ is equal to $\vec{p} \ne \vec{0}$. By rotating the regular n-polygon of $\frac{2\pi}{n}$, we obtain the same polygon. But the sum $S = \vec{p}$ is also rotated $\frac{2\pi}{n}$ and is equal to $\vec{p'}$. We have the vector $\vec{p'} = \vec{p}$ which has a different direction. There is only 1 possibility $\vec{p} = \vec{0}$.

Hence, by absurdity, we proved that $S = \sum_{i=1}^n \vec{OA_i} = \vec{0}$.

Now, just make a remark that, for all $\theta$ \begin{align} S &= \sum_{k=1}^n \vec{OA_i} \\ &= \left(\sum_{k=1}^n \cos \left(\theta + \frac{2\pi k}{n} \right)\right)\vec{e_x} +\left(\sum_{k=1}^n \sin \left(\theta + \frac{2\pi k}{n} \right)\right)\vec{e_x} \\ \end{align}

In particular, for $\theta = 0$, we have $$A_1 = \sum_{k=1}^n \cos \left(\frac{2\pi k}{n} \right) = 0$$ $$A_2 = \sum_{k=1}^n \sin \left(\frac{2\pi k}{n} \right) = 0$$

So, the sum $A_1 + i A_2 = 0$, we can conclude that $$\sum_{k=0}^{n-1} e^{2\pi i\frac{k}{n}}=A_1 + i A_2 = 0$$

Answer 4

Let $$ S=\sum_{k=0}^{n-1}e^{\frac{2k\pi}{n}i}. $$ By the invariant of $S$ of rotation through $e^{\frac{2\pi}{n}i}$, one has $$ e^{\frac{2\pi}{n}i}S=S $$ which implies $S=0$.