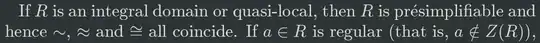Suppose $R$ is a commutative ring with $1$. I would like to get a better understanding of the equivalence relation on $R$ $$x\sim y\iff(x)=(y)\iff\exists u,v\in R,~x=uy~\text{ and }~y=vx$$ where $(x)$ is the principal ideal generated by $x$. Let us also write $$x\approx y\iff \exists u\in R^\times,~x=uy$$ Clearly $x\approx y\implies x\sim y$ holds in any ring.
Question 1. Is there a nice description of $\sim$ equivalence classes as unions of $\approx$ equivalence classes ?
When $R$ is a domain these two equivalence relations are identical. But some non domains also satisfy this property, for instance all rings $\Bbb{Z}/n\Bbb{Z}$ have this property, too. Below we prove moregenerally that rings of the form $R/\mathfrak{a}$ for $R$ PID have this property. This raises the question:
Question 2. Can one characterize the rings $R$ in which the relations $\sim$ and $\approx$ are identical?
One can make some simple observations, for instance $\sim$ equivalence classes agree with $\approx$ equivalence classes when $x$ is $0$, a unit or irreducible. If $x$ is cancellable in the sense that $xu=0\implies u=0$ then the equivalence classes agree, too. If $x\sim y$ and $x$ is nilpotent, then $y$ is nilpotent and $x$ and $y$ have the same nilpotency index, but I'm not sure they are necessarily $\approx$-equivalent.
Question 3. For what types of elements of $R$ do the $\sim$ and $\approx$ equivalence classes agree ?
When $R$ is a domain one has that $x$ is irreducible if and only if $(x)$ is maximal in the set of proper principal ideals of $R$. In a general ring "irreducible implies maximal" holds.
Question 4. What can be said about $x$ if $(x)$ is maximal in the set of principal ideals $<(1)$ ?
Finally, in order to build intuition, I would like to see some examples of non domains where the relations $\approx$ and $\sim$ agree and examples where they disagree.
Question 5. What are some good examples of non domains where the relations $\approx$ and $\sim$ agree? Where they disagree?
Generalizing the example $\Bbb{Z}/n\Bbb{Z}$ of rings where $\approx~=~\sim$
The fact that the $\sim$ and $\approx$ define the same equivalence relation in the rings $\Bbb{Z}/n\Bbb{Z}$ can be generalized:
Lemma. Let $R$ be a PID and $\mathfrak{a}<(1)$ a proper ideal of $R$. Then $\sim$ and $\approx$ are identical in the quotient ring $R/\mathfrak{a}$.
I'm sure there is a more straightforward proof of this, but here goes.
Proof. Since $R$ is a domain there is nothing to prove for $\mathfrak{a}=(0)$. Suppose $(0)<\mathfrak{a}<(1)$ and let $x$ be a generator: $\mathfrak{a}=(x)$. Since PIDs are UFDs we can factor $x$ as a product of irreducibles $x=\prod_{i=1}^np_i^{m_i}$, and so $\mathfrak{a}=(x)=\prod_{i=1}^n\big(p_i^{m_i}\big)$. Since irreducibles are primes in UFDs and nonzero prime ideals are maximal in PIDs, the nonzero prime ideals $(p_i)=\sqrt{\big(p_i^{m_i}\big)}$ are maximal, pairwise distinct and therefore pairwise coprime. It follows that the ideals $(p_i^{m_i})$ are pairwise coprime. The chinese remainder theorem yields $$R/\mathfrak{a}\simeq\prod_{i=1}^nR/\big(p_i^{m_i}\big)$$ Now for any family of rings $(R_i)_{i\in I}$ we have $$\Big(\prod_{i\in I}R_i\Big)^\times=\prod_{i\in I}R_i^\times$$ and for any rings $R_1,\dots,R_n$ the ideals of the product ring are products of ideals: $$ \begin{array}{ccc} \displaystyle \left\{ \text{ideals of } \displaystyle\prod_{i=1}^n R_i \right\} &=& \displaystyle \left\{ \displaystyle\prod_{i=1}^n \mathfrak{a}_i \text{ for ideals }\mathfrak{a}_i\subset R_i \right\} \\ \style{display: inline-block; transform: rotate(-90deg)}{\subseteq} && \style{display: inline-block; transform: rotate(-90deg)}{\subseteq} \\ \displaystyle \left\{ \text{principal ideals of } \displaystyle\prod_{i=1}^n R_i \right\} &=& \displaystyle \left\{ \displaystyle\prod_{i=1}^n \mathfrak{a}_i \text{ for principal ideals }\mathfrak{a}_i\subset R_i \right\} \end{array}$$ These two elementary propositions show that it is enough to prove that $\sim$ and $\approx$ are equal for quotient rings of the form $R/(p^n)$ for primes $p$ and positive $n$.
Thus, let $p$ be a prime of $R$ and $n\geq 1$ a positive integer. The ring $R/(p^n)$ is local and artinian (because noetherian and zero dimensional) and all its ideals are principal. The proof of Theorem 8.5 in Atiyah-MacDonald shows that all its only ideals are the $(0)<\mathfrak{m}^{n-1}<\cdots<\mathfrak{m}<(1)$ for $k=0,\dots,n$ where $\mathfrak{m}=(p)/(p^n)$. Now suppose $(x)=(y)$. Then for some $k$, $(x)=\mathfrak{m}^k$ and so there exists $u$ with $x=up^k$. Since $\mathfrak{m}$ is the only prime ideal in $R/(p^n)$ we have $\sqrt{(0)}=\mathfrak{m}$ and $R/(p^n)=\Big(R/(p^n)\Big)^\times\sqcup \mathfrak{m}$. Therefore, if $u$ were noninvertible it would belong to $\mathfrak{m}$ and so $x\in(p^{k+1})$ whence $(x)\subseteq\mathfrak{m}^{k+1}<\mathfrak{m}^k$ which is a contradiction. Therefore $u$ is invertible. Similarly there exists $v$ invertible with $y=vp^k$ and so $x$ and $y$ are associates.
The paper referenced by @HansLundmark actually contains the preceding and generalizes it: $\sim$ and $\approx$ agree for all quasilocal rings, i.e. rings with only finitely many maximal ideals:
Since the maximal ideals of $R/\mathfrak{a}$ are precisely the $(p_i)/\mathfrak{a}$, $i=1,\dots,n$, quotients of PIDs are quasilocal and thus have the property that $\sim$ and $\approx$ are identical.