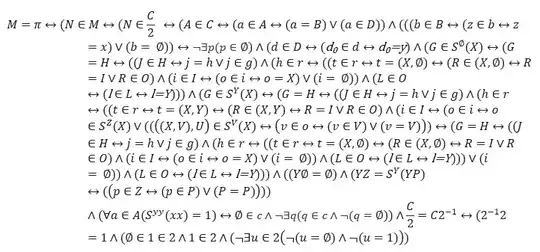15

I know that from ZF we can construct some sets in a beautiful form obtaining the desired properties that we expect to have these sets. In ZF all is a set (including numbers, elements, functions, relations, etc...).

For example we can define a copy of $\mathbb{N}$, using the empty set axiom and others, called sometimes $\omega$ and defining,

\begin{align} 0_\mathbb{N}&=\{\}\\ 1_\mathbb{N}&=\{\{\}\}\\ 2_\mathbb{N}&=\{\{\},\{\{\}\}\}\\ 3_\mathbb{N}&=\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}\\ 4_\mathbb{N}&=\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}, \{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}\}\\ &\ \vdots \end{align}

Well, ZF allow us to build this type of sets that are kind of arrangements of brackets and commas. We can follow with $\mathbb{Z}$ since we can define $(a,b)=\{\{a\},\{a,b\}\}$:

$\mathbb{Z}$ is defined as the set of equivalence classes $\mathbb{Z}=(\mathbb{N}\times\mathbb{N})\big/\sim$ where

$$\sim\, =\{\big((m,n),(h,k)\big)\in(\mathbb{N}\times\mathbb{N})\times (\mathbb{N}\times\mathbb{N}):(m+_\mathbb{N} k)= (h+_\mathbb{N} n)\}$$

here, the integers are sets more complicated than natural numbers. For example,

\begin{align} -2_\mathbb{Z}&=\{(1_\mathbb{N},3_\mathbb{N}),(2_\mathbb{N},4_\mathbb{N}),(3_\mathbb{N},5_\mathbb{N}),\ldots,(n_\mathbb{N},(n+2)_\mathbb{N}),\ldots\}\\ &=\{\{\{1_\mathbb{N}\},\{1_\mathbb{N},3_\mathbb{N}\}\},\{\{2_\mathbb{N}\},\{2_\mathbb{N},4_\mathbb{N}\}\},\ldots\}\\ -2_\mathbb{Z}&=\{\{\{\{\{\}\}\},\{\{\{\}\},\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}\}\},\\ &\quad\{\{\{\{\},\{\{\}\}\}\},\{\{\{\},\{\{\}\}\},\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}, \{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}\}\}\},\ldots\}\\ \end{align}

Here we note the importance of notations. We continue with $\mathbb{Q}=(\mathbb{Z}\times(\mathbb{Z\setminus\{0_\mathbb{Z}\})}\})\big/\sim$ where

$$\sim\, =\{\big((m,n),(h,k)\big)\in(\mathbb{Z}\times(\mathbb{Z\setminus\{0_\mathbb{Z}\})}\})\times (\mathbb{Z}\times(\mathbb{Z\setminus\{0_\mathbb{Z}\})}\}):m\odot_\mathbb{Z}k=h\odot_\mathbb{Z}n\}$$

And for example:

$$(0.2)_\mathbb{Q}=\{(1_\mathbb{Z},5_\mathbb{Z}),(2_\mathbb{Z},10_\mathbb{Z}),(3_\mathbb{Z},15_\mathbb{Z}),\ldots,(n_\mathbb{Z},(5n)_\mathbb{Z}),\ldots\}$$

Imagine if we write the integer numbers as before and write the ordered pairs in unabridged form ($(0.2)_\mathbb{Q}$ is a nice abbreviation for this monster). However we can.

Finally we define $\mathbb{R}$ as the set of all Dedekind cuts, for example:

$$(0.2)_\mathbb{R}=\{x\in\mathbb{Q}:x<_\mathbb{Q} (0.2)_\mathbb{Q}\}$$

Note that $(0.2)_\mathbb{R}$ is even more monstrous than $(0.2)_\mathbb{Q}$. Also I can write $(\sqrt{2})_\mathbb{R}$ showing its elements in a simple form,

$$(\sqrt{2})_\mathbb{R}=\{x\in\mathbb{Q}:(x^2<_\mathbb{Q} 2_\mathbb{Q}) \lor (x<_\mathbb{Q} 0_\mathbb{Q})\}$$

But I don't know how to do it with $\pi_\mathbb{R}$, since

$$\pi=\lim_{k\to\infty}\sum_{n=0}^{k}\cfrac{2^{n+1} n!^2}{(2n + 1)!}$$

I only know that

$$(\pi)_\mathbb{R}=\bigcup_{k=1}^{\infty} \left(\sum_{n=0}^{k}\cfrac{2^{n+1} n!^2}{(2n + 1)!}\right)_\mathbb{R}$$

Since monotonically converge to $\pi$ we have

$$(\pi)_\mathbb{R}=\bigcup_{k=1}^{\infty} \left\{x\in\mathbb{Q}:x<_\mathbb{Q} \left(\sum_{n=0}^{k}\cfrac{2^{n+1} n!^2}{(2n + 1)!}\right)_\mathbb{Q}\right\}$$

Is there any way to avoid infinite union (and the choice of a particular convergent sequence ) as the case of $(\sqrt{2})_\mathbb{R}$? If not, why?

Can we write the set representing $\pi$ listing its elements as we do with integers or rationals (as $\mathbb{Q}$ is countable I guess that should be able to do, but I don't know how to do)?

If in ZF all is a set, is so surprising the fact that so many things can be defined, then my last question is

How many more things can be built using ZF?, ZF could define us what is a derivative, an integral, a limit or a measure?

Thanks in advance.

Gaston Burrull
  • 5,449
  • 5
  • 33
  • 78

4 Answers4

10

Note that when we define the natural numbers we have a good sense of addition and multiplication (ordinal arithmetics), and from those we can define the operations on $\Bbb Z$ and $\Bbb Q$ and then by using Dedekind cuts construction we can extend these to $\Bbb R$ as well.

So we have that $\Bbb R$ has the operations $+,\cdot$ and they all satisfy all the things we know they do from the times we did mathematics without writing all the sets explicitly.

Now we can use these things to start and define anything else that we desire using the $+$ and $\cdot$ and whatnot as our stones. For example you can define $\pi$ to be the length of the semi-circle of radius $1$.

How do we do that? We define what is an integral, and a path integral, and so on. All from the sets which are addition and multiplication and so on, and then we can define $\pi$ in a painfully tedious way.

The whole point of using set theory, and in this case $\sf ZF$, as our foundation is that we can do things, once we can define the real numbers with their basic properties we have formulas which define things from that structure, and we don't have to write everything in set-form explicitly.

Once we have the real numbers (with the order) it is easy to define the collection of open intervals, and then it is easy to define the standard topology (the smallest collection containing the intervals and having certain properties), from there we can define the Borel sets, the Lebesgue sets, and the Lebesgue measure (being the unique function from the Lebesgue sets into the real numbers which satisfies certain properties), then we can define integration and with respect to the measure, and we can define derivation.

All these things end up being immensely long and complicated formulas, but the point is that we can write them up. And all this with just $\in$ and the axioms of $\sf ZF$. (Although we may want to add $\sf DC$ or even $\sf AC$ if we discuss measure theory.)

But if you do want to insist on $\pi$ being written in set form:

$$\pi = \left\{x\in\Bbb Q\mathrel{}\middle|\mathrel{} x<_\Bbb Q0\lor \left(x\geq_\Bbb Q0\land\exists k\in\Bbb N:\frac{x^2}6<_\Bbb Q\sum_{n=1}^k\frac1{n^2}\right)\right\}$$

Asaf Karagila
  • 393,674
3

Let me try this $$(\pi)_{\mathbb{R}}=\left\{x\in \mathbb{Q}:\;\exists k\in\mathbb{N}.\;x< \sum\limits_{n=0}^{k}\cfrac{2^{n+1} n!^2}{(2n + 1)!}\right\}$$ This would be the Dedekind construction of the reals, and note that there is no union here.

Or, I would complete the rationals first by taking the quotient of ring of fundamental sequences with maximal ideal of null sequences $\mathcal{F}_Q/\mathcal{N}_Q$ to obtain a complete field $\mathbb{R}$, then I can safely say that $$\pi=\lim\limits_{k\to\infty}\sum\limits_{n=0}^{k}\cfrac{2^{n+1} n!^2}{(2n + 1)!}$$ (or define exp first, then define sin, then define $\pi$)

mez
  • 10,497
  • It's not quite right to say that only computable numbers can be defined by Dedekind cuts. Being computable is only one way a number can be definable. For example, you could define (via Dedekind cuts) a real number $x$ whose binary expansion codes the halting problem, so $x$ will not be computable. – Trevor Wilson May 24 '13 at 18:10
  • @TrevorWilson How to do code the binary expansion of halting problem via a Dedekind? – mez May 24 '13 at 20:43
  • Say that $x$ is the real number whose binary expansion is $0.d_1d_2d_3 \cdots$ where $d_n=1$ if the $n^\text{th}$ Turing machine halts on input $n$ and $d_n = 0$ otherwise. Then we can define the Dedekind cut ${L,R}$ where $L = {q \in \mathbb{Q} : q < x}$ and $R = {q \in \mathbb{Q} : q > x}$. This is the Dedekind cut representing the number $h$. Note that this argument doesn't depend on some other representation of $x$ as a real number; given a rational number $q$ you can define what the inequality $q < x$ means in terms of the sequence of binary digits $d_1,d_2,d_3\ldots$ of $x$. – Trevor Wilson May 24 '13 at 21:09
  • As you can see, I'm not saying anything nontrivial that is specific to Dedekind cuts. My point was simply that with reasonable notions of computability and definability for any sufficiently complex type of mathematical object (such as binary sequences, or sets of rational numbers) there are going to be definable objects that are not computable. Every computable object is ipso facto definable, but on the other hand there are ways to define things that can't be computed (following Turing.) – Trevor Wilson May 24 '13 at 21:14
  • @TrevorWilson Ok. But is it true that there are only countably many real numbers that is definable by Dedekind cut method? – mez May 24 '13 at 21:45
  • 1
    Yes, only countably many numbers are definable, regardless of how they are represented---whether by Dedekind cuts, Cauchy sequences of rationals, binary expansions, or some other means. The definable real numbers correspond to the definable Dedekind cuts, and the undefinable real numbers correspond to the undefinable Dedekind cuts. – Trevor Wilson May 24 '13 at 21:53
1

It is hard to tell what "Avoid infinite union" means. Of course all dedekind cuts are infinite sets of elements of $\mathbb Q$, which are themselves infinite sets and so on. If you want to write an expression for $\pi_{\mathbb R}$ that avoids blobs of ink looking like $\bigcup_{k=1}^\infty$, you can try to define $\pi$ as smallest positive root of any nonzero function that has a root at zero and is the negative of its second derivative. It may turn out as fun to formulate all this using only rationals.

Hagen von Eitzen
  • 374,180
  • Oops, should of course be infinite. Or I think I was thinking of Cauchy seqeunces while writing the first half of the sentence .. – Hagen von Eitzen May 24 '13 at 07:39
  • "you can try to define π as smallest positive root of any nonzero function that has a root at zero and is the negative of its second derivative. It may turn out as fun to formulate all this using only rationals" I didn't understand what do you mean with this – Gaston Burrull May 24 '13 at 07:40
  • @GastónBurrull with the fun or with the method I sketched? – Hagen von Eitzen May 24 '13 at 07:41
  • your method that you sketched – Gaston Burrull May 24 '13 at 07:42
  • @GastónBurrull: Hagen wrote down a second order ordinary differential equation (in words) whose solutions are $\pm \sin(x)$. – Willie Wong May 24 '13 at 07:45
  • @HagenvonEitzen: I think if you want to formulate ODEs in ZF you will have to first define derivatives and do differential calculus... which makes it annoying (see Asaf's answer also, where he indicated an approach involving developing integral calculus). In any case I'm pretty sure you cannot get by with only using rationals, since $\sin (\mathbb{Q}) \not\subset \mathbb{Q}$, so for functions $\mathbb{Q}\to \mathbb{Q}$ your ODE has no solutions. – Willie Wong May 24 '13 at 07:47
  • @WillieWong thanks I get it, but How is possible using ZF to define what an ODE means? – Gaston Burrull May 24 '13 at 07:48
  • @WillieWong Oh, you answered before. – Gaston Burrull May 24 '13 at 07:49
  • @WillieWong I was thinking of maps $\mathbb Q\to\mathbb Q$ that sufficiently approximate $\sin$ and its ODE. Maybe I'll try to thni it to its end ... – Hagen von Eitzen May 24 '13 at 07:51
  • 2
    @Gaston: The point is that nothing means anything. We mean things, then we write things which express this meaning. We know what is $\pi$ before we start writing the axioms of $\sf ZF$. Later when we have constructed the real numbers in $\sf ZF$ then we know that we have constructed $\pi$ and know that $\pi$ would be a particular number satisfying this and that. We know what ODE means before we try to write in $\sf ZF$, and therefore when we come to write it in $\sf ZF$ we write a huge huge formula stating that this is some sort of particular set with tons of properties. That's all.[...] – Asaf Karagila May 24 '13 at 07:51
  • 1
    [cont.] The point is that we know what we want to do, and we don't have to do it in full explicitness, because once we have established the basic building blocks (i.e. the real numbers with their basic properties) we can prove this and that, and define that and this, and these things have a natural translation to $\sf ZF$ into sets. For example $x\mapsto2^x$ is the unique function which is a group homomorphism from the additive to the positive-multiplicative group of the real numbers which $1\mapsto2$. We can define all these properties, so we can define what is the function $x\mapsto2^x$. – Asaf Karagila May 24 '13 at 07:53
  • 1
    Every time I realize that I have much more to learn, I'm understanding much better because of you @AsafKaragila since your words greatly facilitates my understanding – Gaston Burrull May 24 '13 at 08:05
  • @Gaston: I am very glad to help! – Asaf Karagila May 24 '13 at 08:10
-2

I wrote the original equation in Word and added it here

enter image description here

dantopa
  • 10,342
Master
  • 203
  • 1
  • 11