Atiyah/Macdonald's commutative algebra book asks the reader to draw pictures of the prime spectrum of $\mathbb{Z}$ in exercise 1.16. I worked through it on my own, figured out what the space looks like as a set and where the open/closed sets are, but when I did some research to check my work I found the following picture: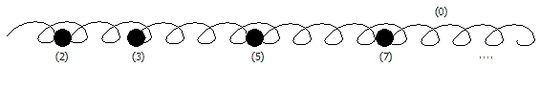
What exactly is the squiggly line supposed to represent? is it meant to be the ideal $(0)$? That makes a vague bit of sense to me, as the closure of (0) is the entire space, but it contradicts the fact that (0) is a single point in the prime spectrum. Another source said to draw $\operatorname{Spec}(\mathbb{Z})$ as a curve passing through the ideals $(2),(3),(5),\ldots$ and a separate point off to the side to represent $(0)$, but again I don't get how drawing a curve helps clarify the structure of the space. Why not draw it as a discrete set of points and leave out the curve?
Edit: Here's another guess I just came up with: If we put the finite-complement topology on the real line and then create a quotient space by identifying every point that is not a prime positive integer as one point and call it (0), do we get $\operatorname{Spec}(\mathbb{Z})$? If this is the case it would definitely help justify the drawing.
