Is it possible to evaluate the integral $I=\int_0^\infty \frac{\sqrt{x}\arctan(x)}{1+x^2}dx$ with residue theorem?

Question

let's consider the following integral

$$I=\int_{0}^{+\infty}{\frac{\sqrt{x}\arctan{x}}{1+x^{2}}\,\mathrm{d}x}$$ I know exactly how to evaluate it with sneaky methods and obtained $I=\frac{\pi\sqrt{2}}{8}(\pi+2\ln{\left(2\right)})$, but would it be possible to evaluate it with contour integration (Residue theorem)? Of course I have done some simple contour integrations before for example a half circle to evaluate $J=\int_{0}^{+\infty}{\frac{\mathrm{d}x}{1+x^{2}}}$, but for some reason I cannot come up with ideas for this.

Thanks in advance.

In case it is possible, I would like to get hints.

Answer 1

We will evaluate a more general integral $$I(a)=\int_0^\infty\frac{\sqrt{x}\arctan{x}}{a^2+x^2}dx$$ where initially we consider $a>1$.

We will do it due to two reasons:

1. We will get more general expression for integral;
2. We want to avoid integration around branch points which coincide with poles (at $x=+-i$). This would be more complicated technically and would not bring any additional value. Because our integrand does not have any peculiarity at $a=1$ the solution can be expanded to any $a$ aftermath.

We will also use the explicite form for $\arctan$: $\arctan(x)=-\frac{i}{2}\log\frac{i-x}{i+x}$. The branch of logarithm is chosen in such a way that we get $\arctan(x)$ on the right half of axis $X$ (on both banks of the cut). We will integrate along the following closed contour (special keyhole):

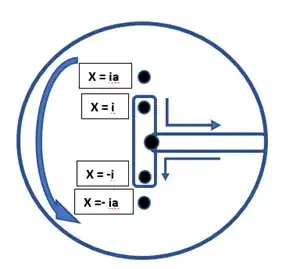
We made two cuts on the complex plane: from $0$ to $\infty$ of the axis $X$ and from $-i$ to $+i$. We go along the upped bank of the cut on $X$, then around a big circle $R$ in the positive direction (counter clockwise), then along the lower bank of the cut on $X$ in the opposite direction and around the cut from $-i$ to $+i$. Logarithm gets an additional factor $+2\pi{i}$ on the left side of the vertical cut when we go around either $x=+i$ or $x=-i$ in the positive direction.

$$\oint_c=\oint_c\frac{\sqrt{x}(-\frac{i}{2}\log\frac{i-x}{i+x})}{a^2+x^2}dx=2I(a)+I_{C1}+I_R$$ where $I(a)$ is the required integral and $I_{C1}$ and $I_R$ are the integrals around the vertical cut and along the big circle correspondingly. While integrating along the contour we have to go along small circles $r$ around points $x=0$, $x=i$ anf $x=-i$. All these integrals $\to0$ at $r\to0$ (and $I_R\to0$ at $R\to\infty$), so further we will not take them into consideration. But we have to care about the additional factors (the integrand phases) which we get when go around these points.

Inside the closed contour the integrand is a single-valued function, therefore $\oint_C=2\pi{i}\sum{Res}\frac{\sqrt{x}(-\frac{i}{2}\log\frac{i-x}{i+x})}{a^2+x^2}$ (residuals at $x=ia$ and $x=-ia$). Evaluation of residuals in not complicated - we just have to bear in mind that (due to the chosen branch of logarithm) logarithm will get an additional factor $\pi{i}$ at $x=a\exp(\frac{\pi{i}}{2})$ (i.e. $x=ia$) and $x=a\exp(\frac{3\pi{i}}{2})$ (i.e. $x=-ia$).

We get: $\oint_C=2\pi{i}\sum{Res}=2\pi{i}\left((-\frac{i}{2})\frac{\sqrt{a}\exp(\frac{\pi{i}}{4})(\log\frac{a-1}{a+1}+\pi{i})}{2ia}+(-\frac{i}{2})\frac{\sqrt{a}\exp(\frac{3\pi{i}}{4})(\log\frac{a+1}{a-1}+\pi{i})}{-2ia}\right)$ $$2\pi{i}\sum{Res}=\frac{\pi}{\sqrt{2a}}\left(\log\frac{a-1}{a+1}+\pi\right)$$

$I_{C1}=\frac{-i}{2}\left(\int_o^{-i}\frac{\sqrt{x}\log\frac{i-x}{i+x}}{a^2+x^2}+\int_{-i}^{0}\frac{\sqrt{x}(\log\frac{i-x}{i+x}+2\pi{i})}{a^2+x^2}+\int_{0}^{i}\frac{\sqrt{x}(\log\frac{i-x}{i+x}+2\pi{i})}{a^2+x^2}+\int_i^0\frac{\sqrt{x}\log\frac{i-x}{i+x}}{a^2+x^2}\right)$. The integrals of logarithms cancel each other; the remaining part is:

$I_{C1}=\pi\left(\int_0^1\frac{i\sqrt{t}\exp(\frac{\pi{i}}{4})}{a^2-t^2}+\int_1^0\frac{-i\sqrt{t}\exp(\frac{3\pi{i}}{4})}{a^2-t^2}\right)=-\sqrt2\pi\int_0^1\frac{\sqrt{t}}{a^2-t^2}dt$.

After easy manipulations the integral can be reduced to $I_{C1}=-\sqrt2\pi\int_0^1\left(\frac{1}{\sqrt{a}-x}+\frac{1}{\sqrt{a}+x}\right)\frac{dx}{2\sqrt{a}}+\sqrt2\pi\int_0^1\frac{dx}{a+x^2}=-\frac{\pi}{\sqrt{2a}}\log\frac{\sqrt{a}+1}{\sqrt{a}-1}+\frac{\pi\sqrt2}{\sqrt a}\arctan{\frac{1}{\sqrt{a}}}$

Finally we get $2I(a)=2\pi{i}\sum{Res}-I_{C1}=\frac{\pi}{\sqrt{2a}}\log\frac{(\sqrt{a}+1)^2}{a+1}+\frac{{\pi}^2}{\sqrt{2a}}-\frac{\pi\sqrt2}{\sqrt a}\arctan\frac{1}{\sqrt{a}}$ $$I(a)=\frac{\pi}{2\sqrt{2a}}\log\frac{(\sqrt{a}+1)^2}{a+1}+\frac{{\pi}^2}{2\sqrt{2a}}-\frac{\pi}{\sqrt{2a}}\arctan\frac{1}{\sqrt{a}}$$ $$=\frac{\pi}{\sqrt{2a}}\Bigl(\log\frac{\sqrt{a}+1}{\sqrt{a+1}}+\arctan\sqrt a\Bigr)$$

At $a=1$ we get the desired result:

$$I(1)=\frac{\pi}{2\sqrt{2}}\log2+\frac{{\pi}^2}{4\sqrt{2}}$$

Answer 2

Notice that : \begin{aligned}I=2\int_{0}^{+\infty}{\frac{x\arctan{x}}{2\sqrt{x}\left(1+x^{2}\right)}\,\mathrm{d}x}&=2\int_{0}^{+\infty}{\frac{x^{2}\arctan{\left(x^{2}\right)}}{1+x^{4}}\,\mathrm{d}x}\\ &=\int_{-\infty}^{+\infty}{\frac{x^{2}\arctan{\left(x^{2}\right)}}{1+x^{4}}\,\mathrm{d}x}\\ I&=\int_{0}^{1}{\int_{-\infty}^{+\infty}{\frac{x^{4}}{\left(1+x^{4}\right)\left(1+x^{4}y^{2}\right)}\,\mathrm{d}x}\,\mathrm{d}y}\end{aligned}

Now we can apply the residue theorem to $ f_{y}:z\mapsto\frac{z^{4}}{\left(1+z^{4}\right)\left(1+z^{4}y^{2}\right)} $, for $y\in\left(0,1\right] $, on the countour $ \mathscr{C}_{R}=\left[-R,R\right]\cup\Gamma_{R} $, where $ R> \frac{1}{y} $ :

We know : \begin{aligned} \int_{\mathscr{C}_{R}}{f_{y}\left(z\right)\mathrm{d}z}&=2\pi\,\mathrm{i}\left(\mathrm{Res}\left(f_{y},\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}\right)+\mathrm{Res}\left(f_{y},-\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}\right)+\mathrm{Res}\left(f_{y},\frac{\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}}{\sqrt{y}}\right)+\mathrm{Res}\left(f_{y},-\frac{\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}}{\sqrt{y}}\right)\right)\\ &=2\pi\,\mathrm{i}\left(\frac{\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}}{4\left(1-y^{2}\right)}-\frac{\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}}{4\left(1-y^{2}\right)}-\frac{\mathrm{e}^{\mathrm{i}\frac{\pi}{4}}}{4\sqrt{y}\left(1-y^{2}\right)}+\frac{\mathrm{e}^{-\mathrm{i}\frac{\pi}{4}}}{4\sqrt{y}\left(1-y^{2}\right)}\right)\\ \int_{-R}^{R}{f_{y}\left(x\right)\mathrm{d}x}+\int_{\Gamma_{R}}{f\left(z\right)\mathrm{d}z}&=\frac{\pi\sqrt{2}}{2\sqrt{y}\left(1-y^{2}\right)}-\frac{\pi\sqrt{2}}{2\left(1-y^{2}\right)} \end{aligned}

We have : $$ \left|\int_{\Gamma_{R}}{f_{y}\left(z\right)\mathrm{d}z}\right|\leq\int_{\Gamma_{R}}{\left|f\left(z\right)\right|\left|\mathrm{d}z\right|}\leq\frac{R^{2}}{\left(R^{4}-1\right)\left(R^{4}y^{2}-1\right)}\int_{\Gamma_{R}}{\left|\mathrm{d}z\right|}=\frac{R^{4}\pi}{\left(R^{4}-1\right)\left(R^{4}y^{2}-1\right)}\underset{R\to +\infty}{\longrightarrow}0 $$

Thus, taking $ R $ to $ +\infty $, we get : $$ \int_{-\infty}^{+\infty}{f_{y}\left(x\right)\mathrm{d}x}=\frac{\pi\sqrt{2}}{2\sqrt{y}\left(1+\sqrt{y}\right)\left(1+y\right)} $$

That means : \begin{aligned} I=\pi\sqrt{2}\int_{0}^{1}{\frac{\mathrm{d}y}{2\sqrt{y}\left(1+\sqrt{y}\right)\left(1+y\right)}}&=\pi\sqrt{2}\int_{0}^{1}{\frac{\mathrm{d}y}{\left(1+y\right)\left(1+y^{2}\right)}}\\ &=\frac{\pi\sqrt{2}}{2}\int_{0}^{1}{\left(\frac{1}{1+y}+\frac{1-y}{1+y^{2}}\right)\mathrm{d}y}\\ &=\frac{\pi\sqrt{2}}{2}\left[\ln{\left(1+y\right)}+\arctan{y}-\frac{\ln{\left(1+y^{2}\right)}}{2}\right]_{0}^{1}\\ I&=\frac{\pi\sqrt{2}}{8}\left(\pi+\ln{4}\right) \end{aligned}