1

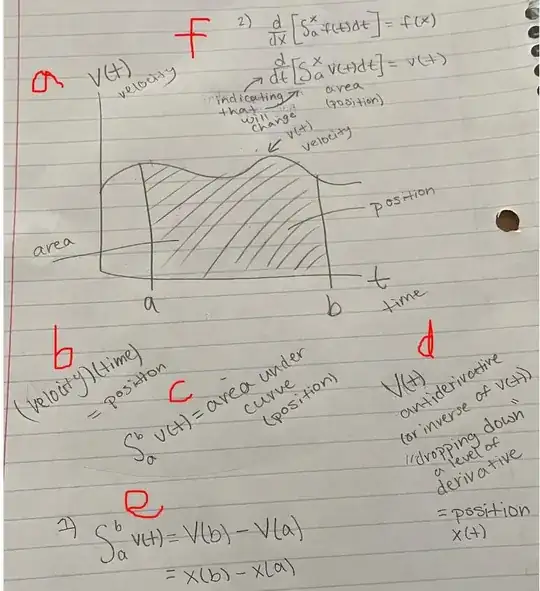
I am not sure that I am completely understanding FTC in terms of how the derivative and definite integral are connected. I drew/wrote this depiction of how I currently think they are connected in terms of velocity and position. I was wondering if anyone could point out any potential gaps in my understanding. enter image description here

Khayla Williams
  • 41
  • 5
    This thread is worth a look: https://math.stackexchange.com/questions/1537821/why-does-the-fundamental-theorem-of-calculus-work – littleO Jan 29 '21 at 17:05
  • 1
    You need to be really careful because the following statement you made is incorrect: $\frac{d}{dt}\left[\int\limits_a^x v(t)dt\right] = v(t)$ because $\left[\int\limits_a^x v(t)dt\right]$ is a function of $x$, not $t$, so, in a since, the technically correct as is $0$ although the "more" technically correct answer is it's $v(x)\frac{dx}{dt}$. – Jared Jan 30 '21 at 00:28
  • I think it's often times very useful to completely write out FTOC when trying to use it, rather than attempting to remember the derivative rule. For instance: $\frac{d}{dt}\left[\int\limits_a^x v(t)dt\right] = \frac{d}{dt}\left(F(x) - F(a)\right)$ where, by FTOC, we know that $F'(x) = v(x)$. Thus when differentiating we employ the chain rule and say $\frac{d}{dt}F(x) = \frac{d}{dx}F(x)\cdot\frac{dx}{dt} = v(x)\frac{dx}{dt}$. – Jared Jan 30 '21 at 00:31

1 Answers1

1

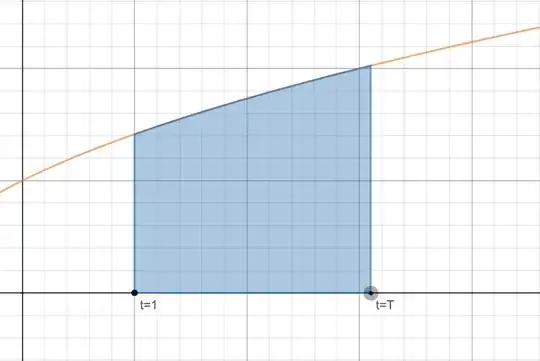
I'd say your geometric picture is a good start for understanding the fundamental theorems of calculus. (I say theorems because really there are two of them.) Say the velocity of a car that has been travelling for one second can be modelled by the equation $$ v(t)=\sqrt{t+1} \quad{1\leq t} \, , $$ The velocity-time graph looks like this:

Velocity-time graph

Since the horizontal axis represents time, and the vertical axis velocity, the area under the curve represents the $\text{velocity $\times$ time $=$ displacement}$ of the car. This means that the displacement of the car (from its position at $t=1$) after $T$ seconds is given by $$ \int_{1}^{T}v(t) \, dt = \int_{1}^{T} \sqrt{t+1} \, dt \, . $$ But we also know that the derivative with respect to time of displacement is the velocity, meaning that the antiderivative of velocity is displacement. That last sentence was a little sloppy: every function has infinitely many antiderivatives which differ by a constant. But we can use the information given in this example to narrow things down to one antiderivative: $$ s(t) = \int v(t)\, dt \, = \int \sqrt{t+1} \, dt = \frac{2}{3}\left(t+1\right)^{3/2}+C $$ When $t=1$, the displacement of the car is zero. Hence, $$ s(1) = 0 = \frac{2}{3}\left(t+1\right)^{3/2}+C \implies C = -\frac{2}{3}2^{3/2} \, , $$ meaning that $$ s(t) = \frac{2}{3}\left(t+1\right)^{3/2} - \frac{2}{3}2^{3/2} \, . $$ Hence, after $T$ seconds, the displacement is given by $$ s(T) = \frac{2}{3}\left(T+1\right)^{3/2} - \frac{2}{3}2^{3/2} $$ But we also know that $$ s(T) = \int_{1}^{T} \sqrt{t+1} \, dt \, $$ which gives us a clue as to how integrals and antiderivatives are related. In more general terms, $$ s(T) = \int_{1}^{T} v(t) \, dt = \int v(t) \, dt \bigg|_{t=T} $$ (Here, I'm using the notation $$ \int v(t) \, dt \bigg|_{t=T} $$ in a slightly unorthodox way, to refer to one particular antiderivative rather than many.) We are almost there: if we differentiate both sides of $$ \int_{1}^{T} v(t) \, dt = \int v(t) \, dt \bigg|_{t=T} \, , $$ we get $$ \frac{d}{dt}\int_{1}^{T} v(t) \, dt = v(T) \, , $$ which is the first fundamental theorem of calculus. We have at last discovered a concrete connection between integrals and antiderivatives. Again, there is a nice geometric interpretation. Recall that by definition, \begin{align} \frac{d}{dt}\int_{1}^{T} v(t) &= \lim_{\Delta t \to 0}\frac{\int_{1}^{T+\Delta t} v(t) \, dt-\int_{1}^{T} v(t) \, dt}{\Delta t} \\[6pt] &= \lim_{\Delta t \to 0}\frac{\int_{T}^{T+\Delta t}v(t) \, dt}{\Delta t} \, . \end{align} As $\Delta t$ shrinks towards zero, the area (marked in green below) $$ \int_{T}^{T+\Delta t}v(t) \, dt $$ is better and better approximated by the rectangle with width $\Delta t$ and height $v(T)$.

Another geometric interpretation

Since $$ \lim_{\Delta t \to 0}\frac{\int_{T}^{T+\Delta t}v(t) \, dt}{\Delta t} $$ is, roughly speaking, the ratio of the area of the rectangle to its width, this limit must be equal to the height of the rectangle $v(T)$, which is what we wanted. If I find the time, I'll try to update this post with more information about the second fundamental theorem of calculus.

Joe
  • 19,636