0

Let $f(n)$ give the number of Collatz iterations it takes to yield a number less than $n$, using the "shortcut" version of Collatz which applies $n\rightarrow (3n+1)/2$ for odds.

Suppose it can be shown that $$f(n)=k \iff f(n+a2^k)=k\qquad \forall a\in\mathbb N.$$

So if a starting value of $n$ decreases, it must happen in at most $2^n$ steps, and then we can say the same thing about that lower number, and so on, summing to a worst case upper bound of $2^{n+1}$ steps.

My question: Is my reasoning correct, and if so, is this a known result?

Per request, the reason I think I can show the above is based on the empirical results for $n<5\times 10^6$, which gives:

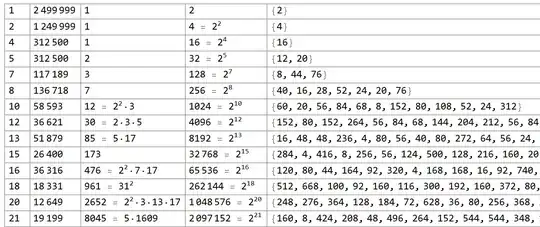
The leftmost column is $k$, the number of steps required to reach a smaller number. The fourth column, obviously going as $2^k$, is the period after which appearances of $k$ repeat. There are multiple appearances of a given $k$ within that period, e.g. for $k=5$ which shows up with alternating intervals of 12 and 20, but that's not required for my conjecture.

This pattern strikes me as regular enough that I suspect a good reason for it would not be hard to work out. Of course, I could be wrong about that, but my question is whether the rest of my logic makes sense assuming a proper proof for this part exists.

In fact, Wikipedia gives "... it can be shown that the parity sequences for two numbers $m$ and $n$ will agree in the first $k$ terms if and only if $m$ and $n$ are equivalent modulo $2^k$." Parity in this context refers to whether a step increases or decreases the number, so if the parity sequences are the same for two numbers, they will indeed both decrease below their original value on the same step number, which seems like it confirms my suspicion that the above is solid, but as Collag3n points out, is not quite proof.

Couple of thoughts on $f(n)=k \iff f(n+a2^k)=k\qquad \forall a\in\mathbb N$:

First, we still assert that $f(n)=k \implies f(n+a2^k)=k$. Then, let $f(n)=j$ and $f(n+2^k)=k$, where $j \neq k$. Note that $f(n)=j \implies f(n+a2^j)=j$.

If $j<k$, then let $a=2^{k-j}$ and we have $f(n+a2^k)=f(n+(2^{k-j})2^j)=j=f(n+2^k)=k$ by the asserted implication, which is a contradiction.

Experimentally, it looks like $f(n+2^m)>m$ until hitting $f(n+2^k)=k$. Note this would give $f(n+2^k)=k\implies f(n+2^{k-1})>f(n+2^k)$.

Trevor
  • 6,022
  • 15
  • 35
  • 1
    Please add proof (or at least some reason) of what you "think you cam show". – coffeemath Jan 29 '21 at 17:25
  • 1
    $f(n)=k \Rightarrow f(n+a2^k)=k\qquad \forall a\in\mathbb N$, but from what I know, the opposite is not proven (https://math.stackexchange.com/questions/2539458/n-0-to-n-i-and-n-0k-cdot2j-ton-ik-cdot3i-same-glide), at least for the definition you gave it (which is not clear either: a lower value or the first lower value?). Also, your conclusion about $2^n$ from this is not clear. – Collag3n Jan 29 '21 at 18:52
  • @Collag3n Yeah, $f(n)$ is the number of steps before the first value $<n$. My largest value claim was just wrong, I think I conflated it with $2^{2^n}$. I'm looking through the link you posted now, interesting food for thought there too... – Trevor Jan 29 '21 at 19:18
  • If you find a proof of $f(n)=k \iff f(n+a2^k)=k\qquad \forall a\in\mathbb N$, I am highly interested. – Collag3n Jan 29 '21 at 19:32
  • 1
    In fact, I don't think that $f(n)=k \Rightarrow f(n+a2^k)=k\qquad \forall a\in\mathbb N$ is proven either. For that you would need to prove that $2^k>3^i \Rightarrow m < n$ (i being the number of odd steps and $m$ the value attained after the $k$ steps). Imagine that is not the case ($2^k>3^i$ and $m>n$), than $n+a2^k$ leads to $m+a3^i$ and there exist a value $a$ for which $m+a3^i<n+a2^k$. Note: the opposite $m < n\Rightarrow 2^k>3^i$ is straightforward from $m=\frac{3^i}{2^k}n+\delta$ and $m+a3^i=\frac{3^i}{2^k}(n+a2^k)+\delta$ – Collag3n Jan 29 '21 at 22:17
  • @Collag3n From https://oeis.org/A126241: "Congruency relationship: For $n>1$ and $m>1$, all $m$ congruent to $n \bmod 2^{a(n)}$ have a dropping time equal to $a(n)$." – Trevor Jan 30 '21 at 02:46
  • I agree that it is well known, but I never saw any proof of that yet. (Note: many times I see OEIS stating unproven things that are most of the time nonetheless true.....most of the time.....). It is linked to the fact that $k={\lceil i\cdot \log_23\rceil}$ which is known but not proven – Collag3n Jan 30 '21 at 07:39

0 Answers0