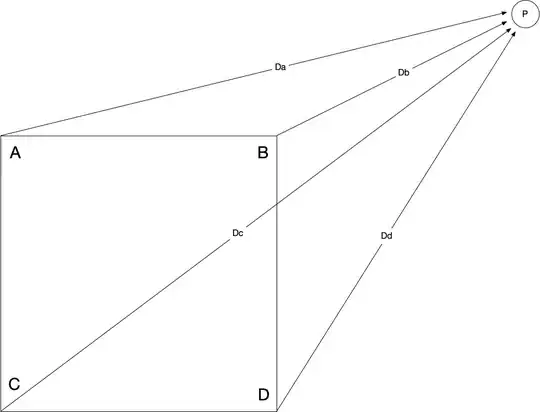
I've got 4 sensors with known positions in a square. Each sensor reports the distance, but not vector, between itself and an object (point P). Unfortuanately the sensors aren't perfectly accurate.
Point P can be anywhere inside or outside the square formed by the sensors.
I'm trying to calculate the best-guess position of the point P.
Diagram of sensors and point
Just to make it a bit more real - the sides of the sensor square are 2 meters and the sensor inaccuracy is between 0 and 15cm.
Thinking about it visually - it feels like it could be the geometric center of the area intersection between donuts drawn around each sensor point.
Doing it visually with donuts
The grey area is where point P could be.