Hyperbolic decay
$$f_\alpha(x)=\frac{1}{\alpha x + 1} $$
is slower than exponential decay
$$f(x) = e^{-x}$$
where $\alpha > 0$ is a scaling factor. The larger that $\alpha$ is, the steeper the descent towards $0$.
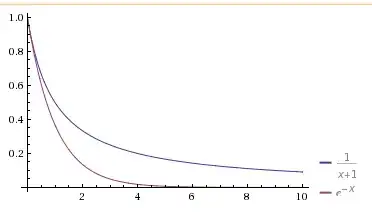
What would be a slower decay function than hyperbolic?