Area bounded by $2 \leq|x+3 y|+|x-y| \leq 4$

Question

Find the area of the region bounded by $$2 \leq|x+3 y|+|x-y| \leq 4$$

I tried taking four cases which are: $$x+3y \geq 0, x-y \geq 0$$ $$x+3y \geq 0, x-y \leq 0$$ $$x+3y \leq 0, x-y \geq 0$$ $$x+3y \leq 0, x-y \leq 0$$ But it becomes so confusing to draw the region. Any better way ?

$f(x)=k$ is a growing trapeze, so the resulting area while be a "trapezoidal ring" https://www.desmos.com/calculator/dl30r7krfn — zwim, Jan 24 '21 at 12:20
It's cheating, but you could just stick it into Wolfram Alpha: https://www.wolframalpha.com/input/?i=draw+2%E2%89%A4%7Cx%2B3y%7C%2B%7Cx-y%7C%E2%89%A44 — Teddy38, Jan 24 '21 at 12:38

Martin R · Accepted Answer · 2021-01-24T12:43:09.593

5

The transformation $$ \begin{align} u &= x + y \\ v &= 2y \end{align} $$ transforms the region $$ 2 \leq|x+3 y|+|x-y| \leq 4 $$ to $$ 2 \leq|u+v|+|u-v| \leq 4 $$ and increases the area by a factor of two (why?). The new region is limited by two squares with side length $2$ and $4$, respectively (compare How to solve $|a+b|+|a-b|=c$?), so that its area can be computed easily.

edited Jan 24 '21 at 12:43

answered Jan 24 '21 at 12:41

Martin R

113,040

1

I like this answer. I knew there was a linear algebra interpretation. – Benjamin Wang Jan 24 '21 at 12:42
why the area is scaled by factor of $2$. ? – Umesh shankar Jan 25 '21 at 02:41
@Umeshshankar: It is a shear mapping $(x, y) \mapsto(x+y, y)$ which preserves the area, followed by scaling in $y$-direction by a factor of $2$. Or you use that it is a linear transformation whose determinant is equal to $2$. – Martin R Jan 25 '21 at 06:09

score 2 · Answer 2 · answered Jan 24 '21 at 12:44

Here is how I would resolve the absolute equations.

$2 \leq|x+3 y|+|x-y| \leq 4$

If $x \geq y,$

$2 \leq|x+3 y|+ x-y \leq 4$

For $x+3y \geq 0, x+3y \leq 0,$ we get

$1 \leq x+y \leq 2, - 1 \leq y \leq -\frac{1}{2}$

Similarly for $x \leq y$, we have

$-2 \leq x+y \leq -1, \frac{1}{2} \leq y \leq 1$

That gives you the below region to find area of,

Finding area may be easier with a transformation and the transformation choice is obvious but given the focus of the question, I am not getting there.

score 1 · Answer 3 · edited Jun 08 '22 at 12:16

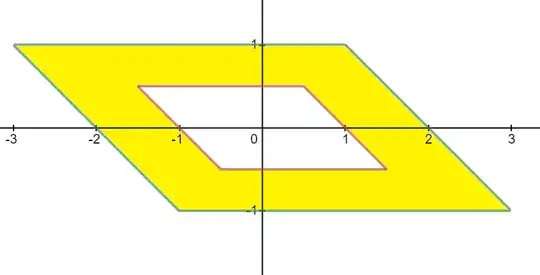
Well, if you're looking for a plot:

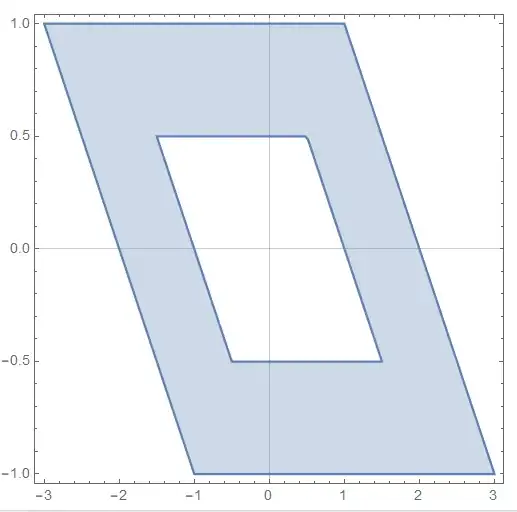
enter image description here

Now, if we want to find the area of the part where $y\ge0$ and $x\ge0$, we can take a look at the following picture:

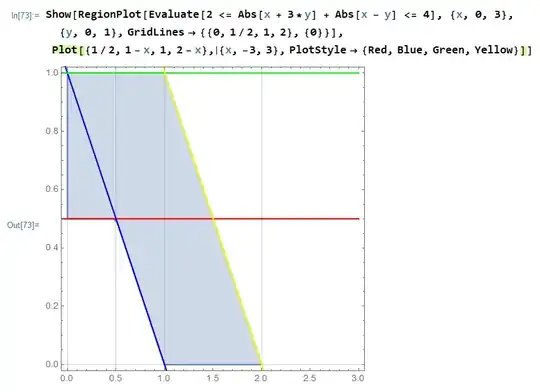
enter image description here

We can find the shaded area by finding:

$$3\cdot\left(\int_0^\frac{1}{2}\left(1-x\right)\space\text{d}x-\frac{1}{2}\cdot\frac{1}{2}\right)+\frac{1}{2}\cdot\frac{1}{2}+\int_1^2\left(2-x\right)\space\text{d}x=\frac{9}{8}\tag1$$

And the place where $y\ge0$ and $x\le0$, we can take a look at the following picture:

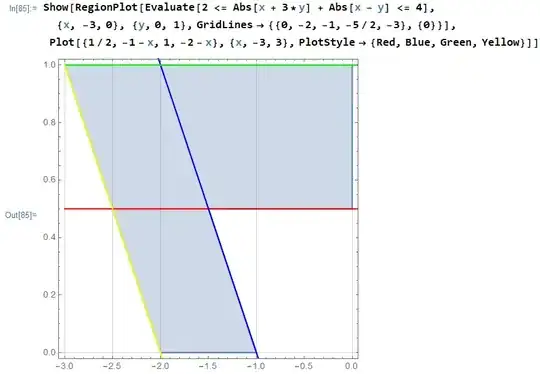
enter image description here

We can find the shaded area by finding:

$$3\cdot\frac{1}{2}\cdot1+\frac{1}{2}\cdot\frac{1}{2}+\int_0^\frac{1}{2}\left(1-x\right)\space\text{d}x-\frac{1}{2}\cdot\frac{1}{2}=\frac{15}{8}\tag 2$$

So, the total area is given by:

$$\mathscr{A}=2\cdot\frac{9}{8}+2\cdot\frac{15}{8}=6\tag3$$

Area bounded by $2 \leq|x+3 y|+|x-y| \leq 4$

3 Answers3