Fibonacci variant with small exponent

Question

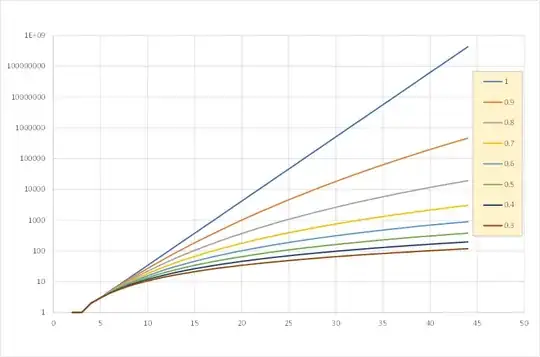
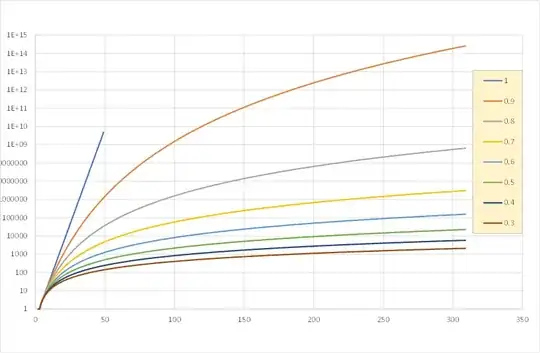
The standard Fibonacci sequence defined by $F(n) := F(n-1) + F(n-2)$ has exponential asymptotic growth as stated e.g. here (with the approximate base being the golden ratio). What happens if the recurrence equation is altered by adding an exponent to $F(n-2)$? Intuitively, instead of 'add the previous number at every step', we get 'add a constant power of the previous number at every step'. I.e.,

$$ F(n) := F(n-1) + F(n-2)^c \;\;\;\;\;\text{ where }\;\;\;\; c \in (0,1) $$

What is the asymptotic growth of such a sequence, assuming starting values are still 0 and 1? (Or if this problem is too difficult, what is the asymptotic growth for $c = \frac12$ specifically?)

Answer 1

The Ansatz $F(n)\sim An^p$ gives$$1\approx\tfrac{A(n-1)^p+A^c(n-2)^{cp}}{An^p}\approx1-\tfrac{p}{n}+A^{c-1}n^{-(1-c)p}-2cpA^{c-1}n^{-(1-c)p-1}.$$We want the penultimate (last) term to scale as $n^{-1}$ ($n^{-2}$), so $p=\tfrac{1}{1-c},\,A=p^{1/(c-1)}$, i.e.$$F(n)\approx(n(1-c))^{1/(1-c)}.$$The $c\to0^+$ behaviour is consistent with @Joffan's answer. A comparison with the exponential $c\to1^-$ result is achievable by noting$$\exp(\alpha n)=\lim_{c\to1}[1+(1-c)\alpha n]^{1/(1-c)}.$$If we want a more precise approximation of $F(n)$, we can define$$\begin{align}\epsilon(n)&:=F(n)(n(1-c))^{-1/(1-c)}-1\\&=[F(n-1)+F(n-2)^c](n(1-c))^{-1/(1-c)}-1\\&=(1-1/n)^{1/(1-c)}(1+\epsilon(n-1))-1\\&+(1+\epsilon(n-2)(n-2)^{1/(1-c)}(1-c)^{1/(1-c)})^c(n(1-c))^{-1/(1-c)}\\&\approx\epsilon(n-1)-\tfrac{n^{-1}}{1-c}+n^{-1/(1-c)}(1-c)^{-1/(1-c)}+c\epsilon(n-2)(1-\tfrac{2n^{-1}}{1-c})\end{align}$$through repeated use of $(1+u)^v\approx1+uv$. In particular, $0\approx\epsilon(n)\approx\epsilon(n-1)+c\epsilon(n-2)$, so $\epsilon(n)\in O((-c)^n)$. In other words, $F$ is a power law plus an exponentially decaying error whose sign alternates.

Answer 2

This modified sequence with $0<c<1$ grows at a rate somewhere between linear and exponential as illustrated by the graph of some values on a log-y scale:

The smaller the exponent, the less the increment will change at one step compared to the previous. The asymptotic behavior should tend towards (nearly) linear.

All such sequences start $0,1,1,2,3$ - the exponent has no effect applied to $0$ or $1$ of course.