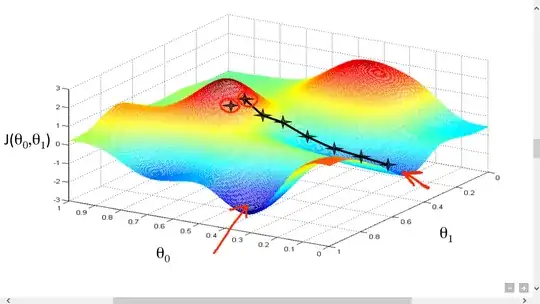
Let's say we start at a wrong "hill" (the highest one), it will find the minimum in that area, but not the whole area? To me it seems, at the moment, that it depends a lot on what m and b we choose at the start.
Asked
Active
Viewed 97 times
4
-
3You don't. That's why gradient descent doesn't work all that well on general non-convex functions. – Rushabh Mehta Jan 22 '21 at 16:26
-
@DonThousand Thank you. Why does it work with image recognition (like written digits)? – hey Jan 22 '21 at 16:47
-
They tend to use one of two techniques: randomized starting points (along with stochastic gradient descent instead of normal gradient descent), because picking enough random starting points on a sufficiently well-behaved loss function should hopefully get you close to the global minimum, or just "convexifying" the loss function. – Rushabh Mehta Jan 22 '21 at 17:08
-
As others have mentioned, indeed there is no guarantee; however, there are several techniques to try to make the result better – Riemann'sPointyNose Jan 22 '21 at 18:25
-
@hey it works since even though you haven't necessarily found the "best solution" (i.e. the weights that give you the global minimum), it's "good enough". Also note, that you can actually get a solution that is "too good" (and begin over-fitting)! – Riemann'sPointyNose Jan 22 '21 at 18:29
1 Answers
3
In short, you don't. Gradient descent only gives you convergence to some local minimum. The first sentence of the wikipedia definition says it gives you a local minimum. In real life examples there often is only a single local minimum and even if there are several, gradient descent will often converge to the gloval minimum but there is no guarantee. As your graph shows, if you try it is not that hard to come up with examples where you get a local minimum which is not the global minimum.
quarague
- 5,921