1

I know how to solve an equation like this and even a bit more complex but only because I've done several exercises like these a while back. In a problem like this I typically just do $dy/dx= b/a$ and get the constant of integration by itself and write $u(x,y)=f(C)$ But I'm realizing that I'm not really understanding what is going on in the geometric (directional derivative solution) sense. I've looked at youtube but nothing satisfactory. I feel like it's a stupidly simple fix or push in the right direction I need. I'm missing something.

Anyways here is a picture:

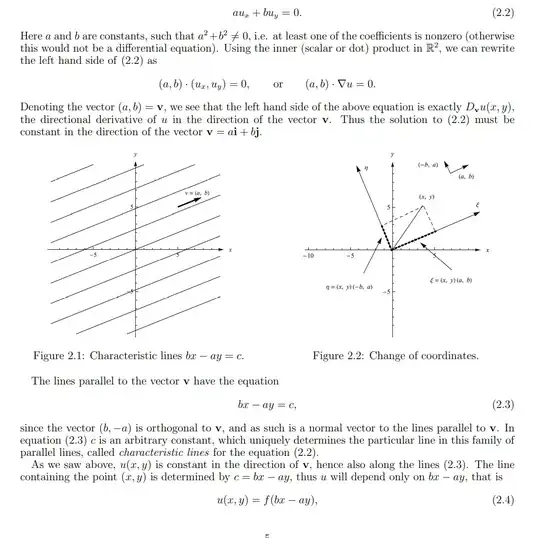
enter image description here

Why do we have $f(bx-ay)$? I understand 2.3 but not 2.4. I don't understand the "line containing the point (x,y)..."

if $(x,y)=(a,b)$ (or any multiple of this vector) we get f(0) but what does that mean? at $(-b,a)$ which is perpendicular to $(a,b)$ we get $f(-b^2-a^2)$. 

Suppose $a=2$ and $b=3$ then $u(x,y)=f(3x-2y)$ . like what is f? I know it's an arbitrary function which needs to be specified initially but it's still a bit confusing. at (1,0) we get u(1,0)=f(3). at another point it changes. how can it be constant? Please provide clarity 

Jama
  • 541

1 Answers1

2

This equation is the transport equation. It might help you if you think of $y$ as time. The solution $u(x,t)$ is constant along the characteristic lines, that is, to find the solution $u(x,t)$ for $t>0$ you just have to travel back in time along the characteristic line passing by the point $(x,t)$. Since the equation is linear, the characteristic are parallel lines, so it is uniquely determined.

To get a well posed-problem (i.e giving a unique solution), you need some information on $u$ at some point $t_0$. Let's say you know $u(x,t_0)=f(x)$, $\forall x \in\mathbb R$. This additional assumption will fix your solution, in the sense that you won't have an infinite number of solutions anymore.

What the fact that $u$ is constant along the characteristics tells us is that to find the value of $u$ at the point $(x,t)$, we just need to travel down the characteristic passing by the point (dotted line in the drawing) until we reach a point $(\bar x, \bar t)$ at which we know the solution. In the pic, I travel down the dotted line until it intersects the $x$ axis because I assumed that we know $u(t=0)=f$. Hence the value of $u(x,t)=f(\xi)=f(ax-bt)$.

Obviously with this approach you can also take a point $(x,t)$ with $t<0$ and travel up the right characteristic to find the solution.

Rem
  • 460
  • I just said that we get f(0). But that's judt the value of the function at 0. It doesn't have to pass at the origin right? The second paragraph overall is a bit confusing. First makes a bit of sense except why are we saying $t>0$. There is no such restriction on $y$ and any point of sign can be found on a line. Also, what do you mean by point on the x-axis that generates the characteristic – Jama Jan 23 '21 at 08:09
  • 1
    @Jama Doesn't have to be $t>0$. In order to find a solution to your equation, you need some kind of knowledge on your solution at some point. What you need here is the \textit{exact} value of $u$ at some point $t_0$, usually $t_0=0$. I willl edit the second paragraph. – Rem Jan 23 '21 at 08:32
  • that helps a lott. Why is your x- coordinate $ax-bt$? – Jama Jan 24 '21 at 09:16
  • Sorry, I think it is given by $\xi = x-\frac abt$. I might have confused $a$ and $b$ in my response. – Rem Jan 24 '21 at 19:07
  • shouldn't $x$ be equal to $b/C$ (we set y or t in your case equal to 0). also can you look at https://math.stackexchange.com/questions/3996403/uniqueness-of-system-of-pde-using-lax-milgram – Jama Jan 26 '21 at 05:41
  • For the characteristic we consider $c = bx - at$ and $b\xi = c$ since both points $(x,t)$ and $(\xi,0)$ are on the same characteristic. Then $b\xi=bx - at \implies \xi = x - \frac abt$. – Rem Jan 26 '21 at 08:46