Substitute $x = \sec u$ to evaluate $\int\sqrt{x^2-1}\ dx$: but why $\tan u= \sqrt{x^2 - 1}$ rather than $\tan u= -\sqrt{x^2 - 1}$ is used?

Question

I tried evaluating $\int\sqrt{x^2-1}\ dx$ using the substitution $x = \sec u$

I know my method gets to the same answer as WolframAlpha, namely:

$$\int\sqrt{x^2-1}\ dx = \frac{1}{2} \left(\ x \sqrt{x^2-1} - \ln\left|x + \sqrt{x^2-1}\right|\ \right) + C,\quad (*)$$

but there is one step I can't justify. When I got to $$\int \tan^2(u)\sec(u)\ du = \frac{1}{2}\left(\ \tan(u)\sec(u) - \ln\left|\sec(u)+\tan(u)\right|\ \right) + C,$$ I then have to substitute stuff back in terms of $x$. Now $$x=\sec(u) \implies \tan^2(u) = x^2 - 1,$$ but I don't see how this implies $\tan(u) = \sqrt{x^2 - 1}$.

Comparing the graphs of $\sec(u)$ and $\tan(u)$, I don't see why not: $\ \tan(u) = -\sqrt{x^2 - 1}$, which would give:

$$\int\sqrt{x^2-1}\ dx = \frac{1}{2} \left(\ -x \sqrt{x^2-1} - \ln\left|x - \sqrt{x^2-1}\right|\ \right) + C,\quad (**)$$

which is a different answer than $(*)$ ?

Now I noticed that $(*) = -(**)\ $ (ignoring the $C \to -C)$.

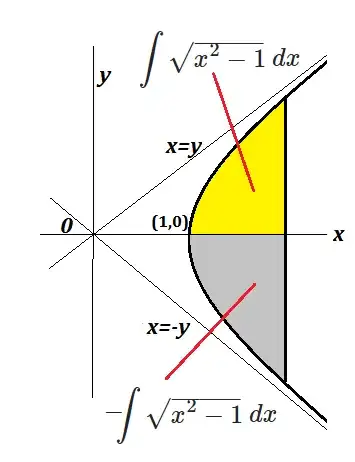
I can see from the graph of $\sqrt{x^2-1}$ that for $x>1$, the definite integral $\int^x_1\sqrt{t^2-1}\ dt = (*),$ and for $x<-1,\ \int^{-1}_x\sqrt{t^2-1}\ dt = (**)$

So is the indefinite integral sort of poorly defined, or would you say it is:

$$\int\sqrt{x^2-1}\ dx = \pm \frac{1}{2} \left(\ x \sqrt{x^2-1} - \ln\left|x + \sqrt{x^2-1}\right|\ \right) + C?$$

Answer 1

I tried evaluating $\int\sqrt{x^2-1}\ dx$ using the substitution $x = \sec(u).$

When I got to $$\int \tan^2(u)\sec(u)\ du = \frac{1}{2}\left(\ \tan(u)\sec(u) - \ln\left|\sec(u)+\tan(u)\right|\ \right) + C,$$

Correction (noting that $\sqrt{\tan^2(u)}=|\tan(u)|$ and that $|\tan(u)|\tan(u)=\operatorname{sgn}(\tan(u))\tan^2(u)$): $$\int\sqrt{x^2-1}\,\mathrm dx\\=\int \color{red}{\operatorname{sgn}(\tan(u))}\tan^2(u)\sec(u)\,\mathrm du \\= \frac{1}{2}\color{red}{\operatorname{sgn}(\tan(u))}\left(\tan(u)\sec(u) - \ln\left|\sec(u)+\tan(u)\right| \right) + C.$$

Now $$x=\sec(u) \implies \tan^2(u) = x^2 - 1,$$

So, $$\tan(u)=\color{red}{\operatorname{sgn}(\tan(u))}\sqrt{x^2-1}.$$

Then, by taking cases and noting, by rationalising denominator, that $$-\ln|x-\sqrt{x^2-1}|\equiv\ln|x+\sqrt{x^2-1}|,$$ this result is obtained:

I know my method gets to the same answer as WolframAlpha, namely: $$\int\sqrt{x^2-1}\ dx = \frac{1}{2} \left(\ x \sqrt{x^2-1} - \ln\left|x + \sqrt{x^2-1}\right|\ \right) + C\quad (*)$$

P.S. Technically, this indefinite integral requires two independent parameters rather than just the one $C$ above.

P.P.S. For definite integration, it will be important that your implicit substitution $x=\sec(u)$ be invertible, typically by restricting it to some choice of principal domain. Alternatively, Quanto's answer makes this explicit at the start of the above, more directly leading to the required answer.

P.P.P.S. If you are comfortable with hyperbolic functions, $x=\cosh(u)$ is a much more elegant and efficient substitution than $x=\sec(u).$

Answer 2

Let's differentiate and see by using which sign we get the integrand. $\begin{align}\frac{d}{dx}\left[\frac{x}{2}\sqrt{x^2-1}-\frac12\ln|x+\sqrt{x^2-1}| + c\right]& = \frac{1}{2}\sqrt{x^2-1}+\frac x2\frac{x}{\sqrt{x^2-1}}-\frac{1+\frac{x}{\sqrt{x^2-1}}}{2(x+\sqrt{x^2-1})}\\ \\& = \frac{2x^2-1}{2\sqrt{x^2-1}}-\frac{1}{2\sqrt{x^2-1}}\\ \\& = \sqrt{x^2-1}\end{align}$

But using the negative sign yields $-\sqrt{x^2-1}$. So the one we've been using is correct.

Answer 3

Whether to utilize $$\tan u = \sqrt{x^2 - 1}\>\>\>\text{or}\>\>\>\tan u = -\sqrt{x^2 - 1}\ $$ depends on the domain of $u$ chosen for the substitution $x=\sec u $. The preferred, yet implicit, choice is $u\in (0,\frac\pi2)\cup (\pi, \frac{3\pi}2)$, which ensures that $\tan u$ is positive, i.e. $\tan u=\sqrt{x^2-1}$. As a result, the integral evaluates to

\begin{align} I=& \ \frac{1}{2}\tan u\sec u -\frac12 \ln\left|\sec u+\tan u\right|\\ =& \ \frac{1}{2} x \sqrt{x^2-1} -\frac12 \ln\left|x + \sqrt{x^2-1}\right| \end{align}

Answer 4

Both are correct, it is a question of recognizing/assigning what goes where.

A radical sign always entails both signs and it should read plus or minus as well as plus and minus.

Note that substitution of $ x\to -x$ in RHS changes the first equation to the second.

$$\int\sqrt{x^2-1}\ dx = + \frac{1}{2} \left(\ x \sqrt{x^2-1} - \ln\left|x + \sqrt{x^2-1}\right|\ \right) + C_1$$

$$\int\sqrt{x^2-1}\ dx = - \frac{1}{2} \left(\ x \sqrt{x^2-1} - \ln\left|x + \sqrt{x^2-1}\right|\ \right) + C_2$$

Also by means of a definite integral we compute both areas, above and below x-axis shown yellow and gray , in geometric areas representation for the equiangular hyperbola:

Answer 5

Another method to do this is, use hyperbolic functions. Consider the change of variables $x=\cosh u$. Then for all $t]x\geq 1$ $$\int_1^x\sqrt{t^2-1}dt=\int_0^{\cosh^{-1}x}\sinh^2 u \;du$$ Since $\cosh(2u)=2\sinh^2u+1$, we have $$\int_1^x\sqrt{t^2-1}dt=\frac12\int_0^{\cosh^{-1}x}\cosh(2u)-1 \;du=\frac14\sinh(2u)-\frac u2$$ Now, $$\frac14\sinh(2u)-\frac u2=\frac12\left(\sinh u\cosh u-u\right)=\frac x2\sqrt{x^2-1}-\cosh^{-1}(x)$$ Hence, $$\int_1^x\sqrt{t^2-1}dt=\frac x2\sqrt{x^2-1}-\cosh^{-1}(x)$$ Note that, for $x\geq 1$, $\cosh^{-1}x=\ln(x+\sqrt{x^2-1})$. Similarly, for all $x\leq -1$ we have, $$\int_{-1}^x\sqrt{t^2-1}dt=\frac x2\sqrt{x^2-1}+\cosh^{-1}(x)$$