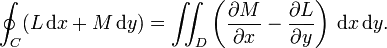Computing the moments of a triangle

Question

Assume you have a triangle in the plane defined by its three vertices at $(x_0,y_0)$, $(x_1,y_1)$, and $(x_2,y_2)$. Is there a general expression for the moments of the triangle, where the moments are defined as averages by the following expression:

$$\langle x^n y^m \rangle = \frac{1}{A}\int_\triangle x^n y^m \, dA $$

Integrating manually to compute the first few moments, one can obtain:

$$\langle x \rangle = \frac{1}{3} \left(x_0+x_1+x_2\right) $$

$$\langle x^2 \rangle = \frac{1}{6} \left(x_0^2+x_1^2+x_2^2+x_0 x_1+x_0 x_2+x_1 x_2\right) $$

$$\langle x y \rangle = \frac{1}{12}\left(2 x_0 y_0+x_1 y_0+x_2 y_0+x_0 y_1+2 x_1 y_1+x_2 y_1+x_0 y_2+x_1 y_2+2 x_2 y_2 \right)$$

Is it possible to obtain a closed form expression for general $n$ and $m$ using combinations of the coordinates?

EDIT:

Can the same be done for line segments defined by their endpoints $(x_0,y_0)$ and $(x_1,y_1)$? Again the first few moments in this case are:

$$\langle x \rangle = \frac{1}{2} \left(x_0+x_1\right) $$ $$ \langle x^2 \rangle = \frac{1}{3} \left(x_0^2+x_0 x_1+x_1^2\right) $$ $$ \langle x^3 \rangle = \frac{1}{4} \left(x_0^3+x_0^2 x_1+x_0 x_1^2+x_1^3\right) $$ $$ \langle x y \rangle = \frac{1}{6} \left(2 x_0 y_0+x_1 y_0+x_0 y_1+2 x_1 y_1\right) $$ $$ \langle x^2 y \rangle = \frac{1}{12} \left( 3 x_0^2 y_0+2 x_0 x_1 y_0+x_1^2 y_0+x_0^2 y_1+2 x_0 x_1 y_1+3 x_1^2 y_1\right)$$

Answer 1

It should be possible using Green's Theorem.

Refer my earlier answer here for more details: Why doesn't a simple mean give the position of a centroid in a polygon?

Answer 2

If you don't mind a quadruple sum as a closed form (it was the best simplification of the integral I gave in the comments that I could manage, using repeated applications of the binomial theorem), then

$\langle x^p y^q\rangle=\displaystyle 2\sum_{k=0}^p\sum_{\ell=0}^q \frac{(-1)^{k+\ell}\binom{p}{k}\binom{q}{\ell}\nu_{k\ell}}{k+\ell+2} x_0^{p-k} y_0^{q-\ell}$

where

$\displaystyle \nu_{k\ell}=\sum_{i=0}^k\sum_{j=0}^\ell \frac{\binom{k}{i}\binom{\ell}{j}}{k-i+\ell-j+1}\left(x_0-x_1\right)^i \left(x_1-x_2\right)^{k-i} \left(y_0-y_1\right)^j \left(y_1-y_2\right)^{\ell-j}$

is an explicit expression for $\langle x^p y^q\rangle$.

FWIW, Mathematica is unable to evaluate this (as usual with such complicated multiple sums).

---

For the problem of finding the moments of a line segment with endpoints $\left(x_0, y_0\right)$ and $\left(x_1, y_1\right)$, the integral can be derived by noting that a set of parametric equations for the line passing through the two given points is

$\displaystyle \begin{align*}x&=x_0+t(x_1-x_0)\\y&=y_0+t(y_1-y_0)\end{align*}\qquad 0\leq t\leq1$

Substituting the two equations into the expression $x^p y^q$ and integrating over the parameter range gives

$\displaystyle \int_0^1\left(x_0+t\left(x_1-x_0\right)\right)^p\left(y_0+t\left(y_1-y_0\right)\right)^q\mathrm{d}t$

which can be expanded into a double sum (again by using the binomial theorem):

$\displaystyle \sum_{j=0}^p\sum_{k=0}^q\frac{\binom{p}{j} \binom{q}{k}}{j+k+1}\left(x_1-x_0\right)^j \left(y_1-y_0\right)^k x_0^{p-j} y_0^{q-k}$

which can be "simplified" into the Appell hypergeometric function:

$x_0^p y_0^q F_1\left(1;-p,-q;2;1-\frac{x_1}{x_0},1-\frac{y_1}{y_0}\right)$