Show that $d/dx (a^x) = a^x\ln a$.

Question

Show that $$ \frac{d}{dx} a^x = a^x \ln a. $$

How would I do a proof for this. I can't seem to get it to work anyway I try.

I know that $$ \frac{d}{dx} e^x = e^x. $$ Does that help me here?

Answer 1

Hint: $a^x=e^{\ln a^x}=e^{x\ln a}$.

Answer 2

Let $f : \mathbb{R} \to \mathbb{R}$ be given by $f(x)=a^x$ and consider the $\ln$ function. We can take the composition so that we have:

$$(\ln\circ f)(x)=\ln (a^x)=x\ln a$$

Now, if we take the derivative, on the left hand side we use the chain rule and on the right hand side we differentiate as usual so that we have:

$$\frac{f'(x)}{f(x)}=\ln a$$

Now solving for $f'(x)$ gives $f'(x) = f(x) \ln a$ so that $f'(x) = a^x \ln a$. This useful technique can be used to take derivatives of other functions: we compose the original function with the inverse and then differentiate on both sides and use the same idea we've used here, this technique can simplify many derivatives and save a lot of time in some situations.

Answer 3

Hint: Write $y = a^x$ or equivalently $\ln y = x \ln a$ and use implicit differentiation.

Answer 4

Here are the steps $$ \frac{d}{dx} \left[a^x\right] = \frac{d}{dx} \left[e^{\ln a^x}\right]= e^{\ln a^x} \frac{d}{dx} \left[\ln a^x\right] $$ $$ = a^x \frac{d}{dx} \left[x\ln a\right] = a^x\left(\ln a\right)\frac{d}{dx} \left[x\right]= a^x\ln a $$

Answer 5

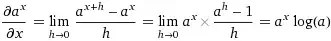, the last term, 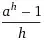, can be explained by L'Hopital's rule, just taking the limits of the numerator and denominator one of each time.

Answer 6

$ \frac{d}{dx} a^x=$

$=d/dx$ $e^{ln\ (a^x)}=$

$=d/dx \ e^{x\ln(a)}$ just as you said.

Now it's time for chain rule.

$f(x)=e^x$

$g(x)=x*ln(a)$

$a^x= f(g(x))$

last comment before I get solving

$a=e^{ln(a)}$

now let's get it done

$d/dx\ e^{x\ ln(a)}=$

$=e^{x*ln(a)}\ d/dx\ (x\ ln(a))=$ (by chain rule)

$=e^{x\ ln(a)} * ln(a)$

and that is the solution. Wait it doesnt look correct --> we should do some algebra!

Show for yourself that

$e^{x*ln(a)}=( e^{ln(a)} )^x$ but as we said that $a = e^{ln(a)}$ so $( e^{ln(a)} )^x$ actually equals $a^x$ and of course $e^{x*ln(a)}$ equals a^x

With what we just said you can see that $e^{x * ln(a)}\ ln(a)$ equals $a^x\ ln(a)$ or

$$d/dx a^x = a^x\ ln(a)$$

Answer 7

Let $y = a^x$

Then taking log on both side to the base $e$

We have;

$ \ln y = \ln a^x$

$ \ln y = x\cdot \ln a$

Taking derivative with respect to $x$;

$\frac d{dx} \ln y = \frac d{dx} x\cdot \ln a$

(I have applied chain rule here>>)

$ \frac 1y \frac{dy}{dx} = \ln a + 0$

$ \frac {dy}{dx} = y\cdot \ln a$

We know $y= a^x$

So, $\frac {dy}{dx} = a^x \ln a$

Hope it was easier than other methodologies used to derive it!