Evaluate $\sum\limits_{r=1}^\infty(-1)^{r+1}\frac{\cos(2r-1)x}{2r-1}$

Question

I would like to know how to evaluate $$\sum\limits_{r=1}^\infty(-1)^{r+1}\frac{\cos(2r-1)x}{2r-1}$$

There are a couple of issues I have with this. Firstly, depending on the value of $x$, it seems, at least numerically, that this value is always $$\pm\sqrt{\frac{\sqrt5-1}{2}}$$ If this is true, how would I prove this?

Secondly, I tried using complex numbers to evalaute this, as shown briefly below:

$$C=\sum\limits_{r=1}^\infty(-1)^{r+1}\frac{\cos(2r-1)x}{2r-1}$$ $$S=\sum\limits_{r=1}^\infty(-1)^{r+1}\frac{\sin(2r-1)x}{2r-1}$$ $$\implies C+iS=\arctan e^{ix}$$ on using the power series of $\arctan x$. Differentiating yields a completely imaginary number: $$\frac{i}{2}\sec x$$ which proves that the value of $C$ is a constant. However, this gives me no information whatsoever on the value of $C$.

Thank you for your help.

Answer 1

As you noted, the real part of the sum, $C$, is constant no matter what the value of $x$ (so long as $x$ is real). Thus plug in $x = 0$

$$C = \operatorname{Re}(\arctan e^{i0}) = \frac{\pi}{4}$$

Answer 2

The Series

This series only converges for $x\in\mathbb{R}$. If $x\not\in\mathbb{R}$, the terms do not go to $0$.$\newcommand{\sgn}{\operatorname{sgn}}\newcommand{\Re}{\operatorname{Re}}\newcommand{\Im}{\operatorname{Im}}$ $$ \begin{align} &\sum_{r=1}^\infty(-1)^{r+1}\frac{\cos((2r-1)x)}{2r-1}\tag{1a}\\ &=\frac12\sum_{r=1}^\infty(-1)^{r+1}\frac{e^{i(2r-1)x}}{2r-1}+\frac12\sum_{r=1}^\infty(-1)^{r+1}\frac{e^{-i(2r-1)x}}{2r-1}\tag{1b}\\ &=\frac12\tan^{-1}\left(e^{ix}\right)+\frac12\tan^{-1}\left(e^{-ix}\right)\tag{1c}\\[9pt] &=\Re\left(\tan^{-1}\left(e^{ix}\right)\right)\tag{1d}\\[12pt] &=\frac\pi4\,\sgn(\cos(x))\tag{1e} \end{align} $$ Explanation:
$\text{(1b)}$: $\cos(x)=\frac12\left(e^{ix}+e^{-ix}\right)$
$\text{(1c)}$: power series for $\tan^{-1}(z)$
$\text{(1d)}$: $\tan(\bar z)=\overline{\tan(z)}$
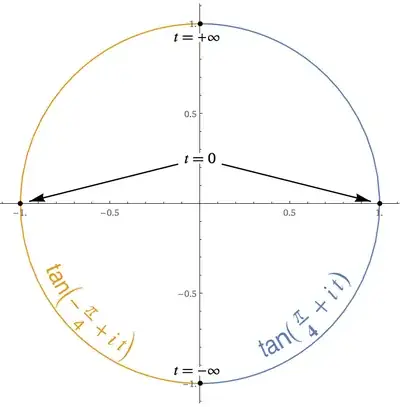
$\text{(1e)}$: $|\tan(z)\,|=1$ when $\Re(z)=\pm\frac\pi4$
$\phantom{\text{(1e):}}$ and $\Re(\tan(z))$ has the same sign as $\Re(z)$
$\phantom{\text{(1e):}}$ also, if $\cos(x)=0$, all the terms of the series are $0$

---

Concerning $\boldsymbol{\tan(x+iy)}$

Note that $$ \begin{align} \tan(x+iy)&=\frac{\sin(x)\cosh(y)+i\cos(x)\sinh(y)}{\cos(x)\cosh(y)-i\sin(x)\sinh(y)}\tag{2a}\\ &=\frac{\sin(x)\cos(x)+i\sinh(y)\cosh(y)}{\cos^2(x)\cosh^2(y)+\sin^2(x)\sinh^2(y)}\tag{2b} \end{align} $$ is on the unit circle when the absolute values of the numerator and denominator are equal. Since $\cosh^2(y)-\sinh^2(y)=1$, equation $\text{(2a)}$ says that is when $$ \begin{align} \sin^2(x)\cosh^2(y)+\cos^2(x)\sinh^2(y)&=\cos^2(x)\cosh^2(y)+\sin^2(x)\sinh^2(y)\tag{3a}\\[6pt] \sin^2(x)&=\cos^2(x)\tag{3b} \end{align} $$ Thus, $|\tan(z)\,|=1$ when $\Re(z)=\pm\frac\pi4$

Furthermore, equation $\text{(2b)}$ says not only that $\tan(\bar z)=\overline{\tan(z)}$, but also that, when $\Re(z)=\pm\frac\pi4$, $\Re(\tan(z))$ has the same sign as $\Re(z)$.

Answer 3

I've learned some new related facts since posting the question, one of which solves this very simply. The relevant formula, stated below, can be found by using the fact $\arctan z=-i\operatorname{artanh} iz$. $$\arctan(x+iy)=\frac{1}{2}\arctan\frac{2x}{1-x^2-y^2}+\frac{i}{2}\operatorname{artanh}\frac{2y}{1+x^2+y^2}$$ Plugging in $x=\cos x$ and $y=\sin x$ we find that $$\arctan e^{ix}=\frac{1}{2}\arctan(\pm\infty)+\frac{i}{2}\operatorname{artanh}\sin x$$ And thus $$C=\pm\frac{\pi}{4}$$