Why are the values of $\sin (\theta)$ and $\csc(\theta)$ positive in the second quadrant?

Question

Why is the value of $\sin (\theta)$ and $\csc(\theta)$ positive in the second quadrant? Similarly why the value of other trigonometric ratios so in other quadrants?

Answer 1

The reason is that the sine is the projection of the point on the trigonometric circle with curvilinear abscissa $\theta$. As to the cosecant, it is the reciprocal of the sine.

Answer 2

First of all note that the cosecant is just $\frac{1}{\sin\theta}$, so they are both positive or both negative.

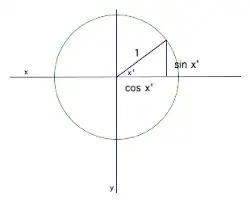
In the second you can view the sin of $\theta$ as the value of the vertical segment that is perpendicular to the $X$ axis drawn from the point where the radios of angle $\theta$ cuts the unit circle, as the figure shows:

Thus, sine is positive in the first two quadrants, but negative in the last two.

Answer 3

You may recall this image:

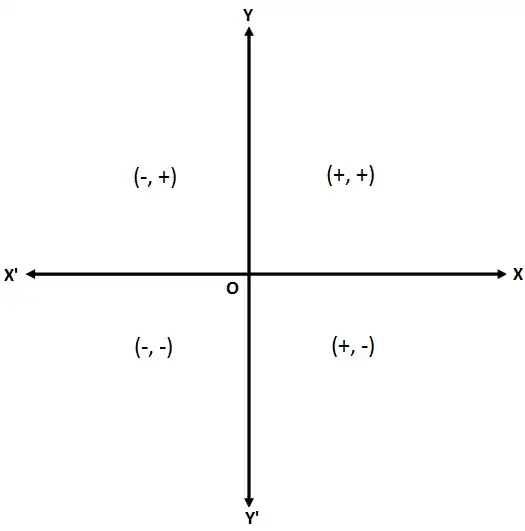
Now, the unit circle definition tells us that $\cos \theta$ and $\sin\theta$ are the $x$ and $y$ coordinates of the point whose radius makes angle $\theta$ with the positive $x$-axis.

Therefore, in the first quadrant ($0<\theta<90^\circ$), both $\cos\theta$ and $\sin\theta$ are positive, and in the second quadrant ($90^\circ<\theta<180^\circ$), $\cos\theta$ is negative and $\sin\theta$ is positive, and so on for third and fourth quadrants.

Define: $$\sec\theta=\frac{1}{\cos\theta}\text{ and }\csc\theta=\frac{1}{\sin\theta}$$ Thus, the sign of $\sec\theta$ is the same as $\cos\theta$ and the sign of $\csc\theta$ is the same as $\sin\theta$.

Define: $$\tan\theta=\frac{\sin\theta}{\cos\theta}\text{ and }\cot\theta=\frac{\cos\theta}{\sin\theta}$$ Thus, the signs of $\tan\theta$ and $\cot\theta$ are positive, if $\sin\theta$ and $\cos\theta$ have same signs, and negative, if different.

For example, for the second quadrant, $\cos\theta$ is negative and $\sin\theta$ is positive. So, $\sec\theta$ is negative and $\csc\theta$ is positive, and , $\tan\theta$ and $\cot\theta$ are negative.

Hope this helps. Ask anything if not clear :)

Answer 4

That's because cartesian coordinate system is defined in that way. This needs explanation, I know.

We have generalised trigonometry, from only inputs between $0$ and $90$ to any real number $\theta$, by using a unit circle (Wikipedia link) on cartesian coordinate system with its centre on origin i.e. $(0,0)$.

To do this generalisation we define $\sin (\theta)$ as $y-axis$ of the the end of the point on radius of that unit circle (Khan Academy link). Now it is by definition that in $2nd$ and $1st$ quadrant $y-coordinate$ is positive, so clearly it follows that $sine$ function must be positive in $2nd$ and $1st$quadrant as it is $y-axis$. Now since $\sin (\theta)$ is positive, so must be $\csc(\theta)$. As we have defined it as reciprocal of $\sin (\theta)$, now reciprocal of any positive number must be a positive number($0$ is not positive).

Now we have similarly defined $\cos(\theta)$ as the $x-coordinate$ of the the end of the point on radius of that unit circle, similarly it must be positive in $1st$ and $4rth$ quadrant. Following image may be helpful:

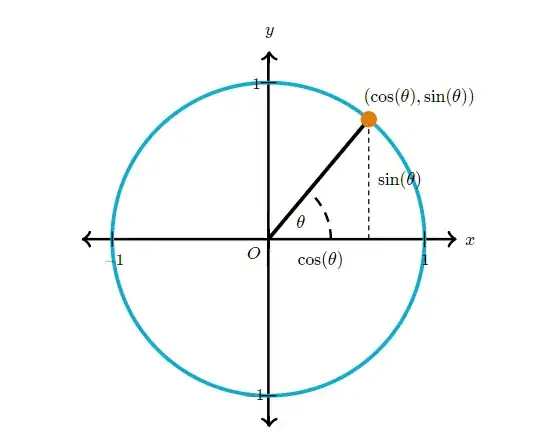
It is left as an exercise for you to find why other trigonometric functions ..... you understand what I mean(right)!