Is This Proof of Pythagorean Theorem?

Question

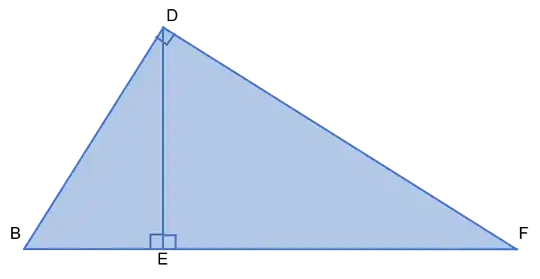
1. Given image:
2. $\triangle\mathit{BDE}$ is an altitude right triangle as given by the image.
3. $\triangle\mathit{BDE}$ and $\triangle\mathit{FDE}$ both contain 90° given by the image; therefore, $\triangle\mathit{BDE}$ and $\triangle{\mathit{FDE}}$ are both right triangles.
4. $\triangle\mathit{BDE}$ is an altitude right triangle with $\triangle\mathit{FDE}$ as given by the image; therefore, $\triangle\mathit{BDE}\sim\triangle\mathit{FDE}$
5. If $\triangle\mathit{BDE}$ is similar to $\triangle\mathit{FDE}$ then:
   • If these triangles are similar, then the ratio of each of the sides of $\triangle\mathit{BDE}$ to the corresponding sides of $\triangle\mathit{FDE}$ is common; therefore, the equations below can be derived:
   • $\overline{\mathit{DE}}^{2}=\overline{\mathit{BE}}\overline{\mathit{EF}}$
   • $\overline{\mathit{DF}}^{2}=\overline{\mathit{EF}}\overline{\mathit{BF}}$
6. $\overline{\mathit{BE}}+\overline{\mathit{EF}}=\overline{\mathit{BF}}$ as given by the image
7. Given these equations algebra can then be performed to solve for $\overline{\mathit{DF}}$. Algebra:
   • Rearranging:$\overline{\mathit{DE}}^{2}=\overline{\mathit{BE}}\overline{\mathit{EF}}$ to get $\frac{\overline{\mathit{DE}}^{2}}{\overline{\mathit{EF}}}=\overline{\mathit{BF}}.$
   • $\overline{\mathit{DF}}^{2}=\overline{\mathit{EF}}\overline{\mathit{BF}}$
   • Substituting:$$\overline{\mathit{DF}}^{2}=\overline{\mathit{EF}}(\overline{\mathit{BE}}+\overline{\mathit{EF}})$$
   • Substituting Again:$$\overline{\mathit{DF}}^{2}=\overline{\mathit{EF}}(\frac{\overline{\mathit{DE}}^{2}}{\overline{\mathit{EF}}} + \overline{\mathit{EF}})$$
   • Simplifying:$$\overline{\mathit{DF}}^{2}=\overline{\mathit{DE}}^{2}+\overline{\mathit{EF}}^{2}$$

Which is the familiar form of Pythagorean Theorem.

Is this a mathematically correct derivation?
Is this proof general enough to be used as a general proof?

Answer 1

OK here's a bit of criticism, meant in the spirit of improvement. Reworking the steps of your attempted proof with the same numbering (plus some commentary):

1. (Your diagram is hard to read; the letters are very small relative to the diagram. I suspect you were sometimes misreading it yourself. The square angle mark is a useful device for avoiding too many numbers:)
   

2. $\triangle BDF$ is a right triangle with right angle at $D \quad$ - (introduce the main triangle)
   $DE\;$ is the altitude from $D$ to $E$ on $BF$, perpendicular to $BF \quad$ - (key construction line)
   $ $ - (I didn't really understand what you were trying to set up in point 2)

3. $\triangle BDE$ and $\triangle FDE $ both contain $90^\circ$ by construction; therefore, $\triangle BDE$ and $\triangle FDE$ are both right triangles.
   $ $- (basically OK, could go into next point)

4. $\triangle BDE$ shares the angle at $B$ with $\triangle BDF$ and both are right triangles, therefore $\triangle BDE \sim \triangle BDF$. In the same way $\triangle DEF$ shares the angle at $F$ with $\triangle BDF$ so $\triangle DEF\sim \triangle BDF$. Thus also $\triangle BDE \sim \triangle DEF$.
   $ $ - (You did not establish this similarity - it works via the main triangle, and the fact that a right triangle can be cut into two similar triangles is key)

5. Thus the ratio between sides of $\triangle DEF$ and the corresponding sides of both $\triangle BDE$ and $\triangle BDF$ are equal, giving:

• $\frac{|DE\,|}{|BE\,|} = \frac{|EF\,|}{|DE\,|} \implies |DE|^2 = |EF|\cdot |BE|$
• $\frac{|DF\,|}{|BF\,|} = \frac{|EF\,|}{|DF\,|} \implies |DF|^2 = |EF|\cdot |BF|$
  $ $ - (No need to say "if $P$" for something you've established; "since $P$" works but it's implied anyway. You neglected to note that one of your ratios here was with the main triangle. Having said you're equating ratios, you should probably do that explicitly. You were using vector-style notation for scalar length.)

6. Note that $|BE|+|EF| = |BF| \quad$
   $ $- (I might have said this back in point 2 when we split $BF$ )

7. Then: \begin{align}|DF|^2 &= |EF|\cdot \left(|BE|+|EF|\right) \\[1ex] |DF|^2 &= |EF|\cdot \left(\frac{|DE|^2}{|EF|}+|EF|\right) \\[1ex] |DF|^2 &= |DE|^2+|EF|^2 \end{align} as required since $\triangle DEF \sim \triangle BDF$.
   $ $- (You can usually just let the equations speak for themselves but linking words here or there are OK. For more involved arguments, equation numbering is very helpful. Probably the link back to the main triangle through similarity should be stated here.)

---

---

Clean version with a variation from your point 5 to solve direct for the main triangle:

$\triangle BDF$ is a right triangle with right angle at $D$ - construct altitude $DE\;$ from $D$ to $E$ on $BF$; this is perpendicular to $BF$ and note that $|BE|+|EF| = |BF|$.

$\triangle BDE$ and $\triangle BDF$ share the angle at $B$ and both are right triangles, therefore $\triangle BDE \sim \triangle BDF$. In the same way $\triangle DEF$ shares the angle at $F$ with $\triangle BDF$ so $\triangle DEF\sim \triangle BDF$.

Thus the ratio between sides of $\triangle BDF$ and the corresponding sides of both $\triangle BDE$ and $\triangle DEF$ are equal, giving:

• $\frac{|DB\,|}{|BF\,|} = \frac{|BE\,|}{|DB\,|} \implies |DB|^2 = |BF|\cdot |BE|$
• $\frac{|DF\,|}{|BF\,|} = \frac{|EF\,|}{|DF\,|} \implies |DF|^2 = |BF|\cdot |EF|$

Then: \begin{align} |DB|^2 + |DF|^2 &= |BF|\cdot |BE| + |BF|\cdot |EF| \\ &= |BF|\cdot \left(|BE|+|EF|\right) \\ &= |BF|^2 \end{align} as required.