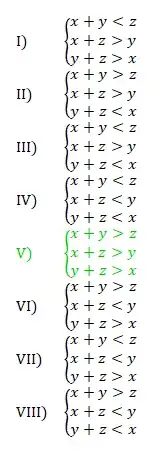-4

I have read a problem which says:

"Consider a segment of length $10$. Points $A$ and $B$ are chosen randomly such that $A$ and $B$ divide the segment into three smaller segments. What is the probability that the three smaller segments could form the sides of a triangle?"

I have checked the solution explanation. It was TOTALLY convenient to me, (simply begin with the triangle inequality which states that the sum of the lengths of any two sides must be greater than the length of the third side). Very well understood.

Here is the solution (taken from the book):

enter image description here

However, I was trying to solve it by another way, there must be a mistake, but I did not find where is that mistake:

THE WRONG SOLUTION:

Let us assume that the three segments are $x,y,$ and $z$.

Now we have $8$ possibilities to have inequalities that relate $x+y$ with $z$, relate $x+z$ with $y$, and relate $y+z$ with $x$. These $8$ possibilities are:

enter image description here

The possibility (V) is the only valid possibility. Hence the required probability is $\frac{1}{8}$.

One may say because of duplicate counting, if that is the mistake, please clarify where is that duplicate.

Your help would be appreciated. Thanks.

KReiser
  • 65,137
Hussain-Alqatari
  • 5,065
  • 2
  • 13
  • 39
  • 6
    Not all of your 8 possibilities have the same probability. In fact several of them aren't possible at all, since e.g. $x + y < z$ implies that $z$ is the largest of the three, and $x + z < y$ implies that $y$ is the largest. – Ravi Fernando Jan 10 '21 at 05:58

1 Answers1

1

As noted already in a comment, for three non-negative numbers $a,b,c,$ an inequality of the form $a+b<c$ implies that $c$ is the unique greatest number among the three, that is, $c>a$ and $c>b.$ It is impossible to have more than one unique greatest number within a list of three numbers, so all the cases with more than one $<$ relation in them are impossible.

The cases with exactly one $<$ are I ($z$ is greatest), II ($x$ is greatest), and VI ($y$ is greatest).

It is also possible to have a greatest side that is not greater than the sum of the other two; this is case V.

So we have four cases, one of which forms a triangle, so you might jump to the conclusion that the probability is $\frac14.$ But let's not be so hasty!

We cannot determine a probability from these four cases because we have not shown any reason to believe that they are equally likely. And indeed there is no reason to believe the four cases are equally likely until we have explicitly specified how we "randomly" choose to break the stick. There are at least two well-known ways to randomly break a stick in three pieces, and they give different answers.

One way to break a stick in three pieces is to choose a number uniformly between $0$ and $10,$ measure that distance from the left end of the stick, and mark point $A$ at the measured distance. Then choose another number uniformly between $0$ and $10,$ independently from the first number, and mark point $B$ at that measured distance from the left end of the stick. This can be represented by the sample space $\{(u,v) \in \mathbb R\mid 0\leq u\leq 10, 0\leq v\leq 10\},$ which is a square.

Another way to break a stick in three pieces is first to break the stick in two pieces as in the procedure above and then choose one of those two pieces at random and break it at a point chosen uniformly along the length of that piece. If $u$ is the distance where the first break is made and $v$ is the distance where the second break is made then the sample space again is at least the square $\{(u,v) \in \mathbb R\mid 0\leq u\leq 10, 0\leq v\leq 10\}.$

A third way is to choose a number $x$ uniformly between $0$ and $10,$ break the stick at that distance from the left end; then choose a number $y$ uniformly between $0$ and $10 - x,$ and from the piece of length $10 - x$ measure a distance $y$ from one end and break the stick there. In other words, we follow the second procedure described above, but after the first break we always take the "right-hand" piece to break again instead of choosing randomly between the two pieces. This can be represented by the sample space $\{(x,y) \in \mathbb R\mid 0\leq x\leq 10, 0\leq y\leq 10 - x\},$ which is the same as $\{(x,y) \in \mathbb R\mid x + y \leq 10, x \geq 0, y \geq 0\},$ which is essentially the sample space shown in the book. (I have $\leq$ where the book has $<$, but the entire set of extra outcomes allowed by $\leq$ has probability zero, so this makes no difference in the answer.) It is not hard to show by symmetry that this procedure results in a triangle with the same probability as the second procedure.

Now I find the answer in the book to be very fishy, because it constructs a sample space that looks like my third example (and not like the first example), represents that sample space graphically as a triangle, and then assumes that the probability distribution over the triangle is uniform without explaining why we should believe it is uniform. In fact, if the stick is broken randomly according to the third procedure I gave, the distribution over the triangle is not uniform and the probability is not $\frac14$.

The probability of a triangle is $\frac14$ if we use the first procedure to break the stick randomly. This is proved in an answer to a previous question (for a stick of length $1$). You might notice that this proof rests on a graphical visualization that looks quite a bit like the one in the book, except that its sample space is a square rather than a triangle and the pattern of subregions within the triangle is duplicated. We actually have a valid reason to think the distribution over the square is uniform (because it was produced by choosing each coordinate uniformly and independently between $0$ and the length of the stick).

David K
  • 98,388