How can you behold that a 45 degree line's |x-intercept| = |y-intercept|?

Question

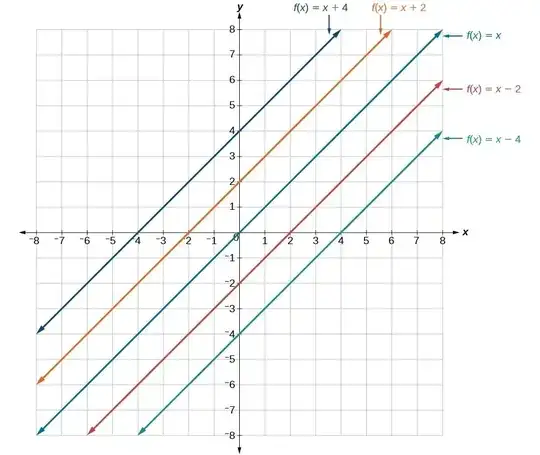
I'm not asking for an algebraic explanation...I can do algebra. I know $f(x) = x - c = 0 \iff x = c$. Right now, I have to make my mind process four steps. First, a line with slope $|1|$ must angle 45° with the y-intercept. Second, I must consider the right triangle bound by $y = x$ and $y = 1, 0 \le x \le 1$ and $x = 0, 0 \le y \le 1$. Third, the remaining angle must be $180 - 90 - 45 = 45°$. Thus the triangle is isoceles, and the opposite and adjacent sides have the same length. Fourth, this means $\mid x-intercept\mid = \mid y-intercept \mid $.

I don't know why, but I can't "behold" immediately this. How can I eye-ball all this quickly?

Answer 1

Because a 45-45-90 triangle is isosceles.

Answer 2

The line segment $y = 1$ for $0 \leq x \leq 1$ seems to me to be completely unnecessary and unhelpful to think about.

For the line $y = x + 4$ the triangle to look at is the green triangle in the figure below. For the line $y = x - 2$ the triangle to look at is the black triangle.

For these two lines, the triangles are isosceles with the equal legs on the $x$ and $y$ axes. Note that $x$ and $y$ intercepts are not equal: they are of equal magnitude (same distance from the origin) but have opposite signs. For example, for $y = x + 4$ the $x$-intercept is $-4$ but the $y$-intercept is $4$.

For $y = x,$ of course, there is no triangle. The line passes straight through the origin, so it intercepts both axes at the same point, $(x,y) = (0,0)$.

For any other line of the form $y = x - c,$ the triangle is again an isosceles triangle with the apex at the origin like the green or black triangles, but possibly larger or smaller.