$X_1,X_2$ distributed $U(0,1)$ and independent, find the distribution of $D=|X_2-X_1|$

Question

I know it shouldn't be this hard but I am having trouble anyway.
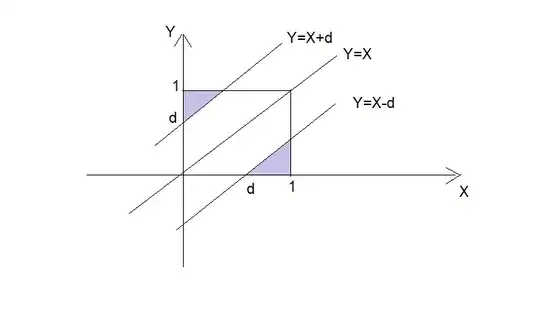
I tried using $F_D(t)=\mathbb{P}(|X_2-X_1|\leq t)=\mathbb{P}(-t\leq X_1-X_2\leq t)$ and sketching the unit square $[0,1]^2$ but to no avail, I can't seem to find a formula that fits.

Answer 1

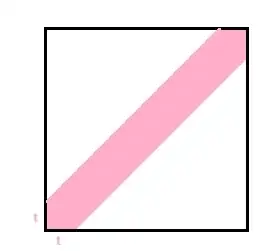
If you to a drawing of the problem it will be very easy to find

$$F_D(d)=1-(1-d)^2$$

and derivating you get the density

$$f_D(d)=2(1-d)\cdot \mathbb{1}_{[0;1]}(d)$$

---

The CDF is the white area, in function of $d \in [0;1]$ To calculate it, it is easier to calculate the purple area $(1-d)^2$ and take the complement to 1

Answer 2

What is the pink area in this unit square?

Answer 3

Sketch for the solution: setting $Z:=(X,Y)$ you will have that $$ \begin{align*} \Pr [|X-Y|\leqslant c]&=\Pr [Z\in A_c]\\&=\int_{\mathbb{R}^2}\mathbf{1}_{A_c}(x,y)f_X(x)f_Y(y)\mathop{}\!d (x,y)\\ &=\int_{[0,1]^2}\mathbf{1}_{A_c}(x,y)\mathop{}\!d (x,y) \end{align*} $$ where $A_c:=\{(x,y)\in \mathbb{R}^2:|x-y|\leqslant c\}$ and $f_X(t)=f_Y(t)=\mathbf{1}_{[0,1]}(t)$ are the densities of $X$ and $Y$. Now observe that

$$ \mathbf{1}_{A_c}(x,y)=1 \iff |x-y|\leqslant c \iff x-y\in[-c,c]\iff y\in \mathbb{R}\,\land\, x\in [y-c,y+c] $$

Therefore $\mathbf{1}_{A_c}(x,y)=\mathbf{1}_{\mathbb{R}}(y)\mathbf{1}_{[y-c,y+c]}(x)$, and so substituting in the last integral we find that

$$ Pr[|X-Y|\leqslant c]=\int_0^{1}\int_0^{1}\mathbf{1}_{[y-c,y+c]}(x)\mathop{}\!d x\mathop{}\!d y $$

Now the inner integral is just the Lebesgue measure of the set $[0,1]\cap [y-c,y+c]$, this is $1-(y-c)$ when $y-c\in[0,1]$ or $y+c$ when $y+c\in[0,1]$, therefore

$$ Pr[|X-Y|\leqslant c]=\int_0^{1}((1-y+c)\mathbf{1}_{[c,c+1]}(y)+(y+c)\mathbf{1}_{[-c,1-c]}(y))\mathop{}\!d y $$