How does the compound angle formula for sine apply to obtuse, reflex and negative angles?

Question

My teacher showed us a proof for the compound angle formula by using a triangle and dropping a perpendicular line from an angle then getting the area of the triangle using sine rule (1) then getting it again by adding the area of the other two triangles (2) (created from the perpendicular line) then making (1) and (2) equal to each other.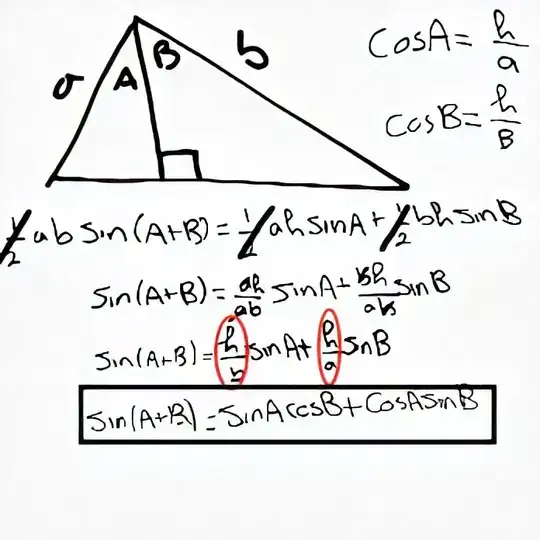

I totally get the proof but not how it can be applied to obtuse, reflex and negative angles. I know about unit circle and how obtuse and reflex angles have sine just as their abtuse equivalent angles but I still don't get it. A visual proof will be tremendously appreciated!

See my answer here, which generalizes my figure in this answer to non-acute angles. — Blue, Jan 05 '21 at 20:38
Wait until you make the connection between trigonometry and complex multiplication -- then it becomes obvious in the general setting without any sweating. — Allawonder, Jan 06 '21 at 05:37
Here is one that derives cos(A-B) using arbitrary angles and then develops the others. Scroll down to "Trigonometric functions of compound angles". — robert timmer-arends, Jan 06 '21 at 10:49

score 0 · Answer 1 · answered Jan 06 '21 at 05:13

A visual proof for obtuse/reflex angles in a triangle? I am not sure such thing exists(specifically for a triangle) but we can generalize the result by taking into account the fact that any angle(obtuse/reflex) can be reduced to a compound angle which I believe you are aware of.

How does the compound angle formula for sine apply to obtuse, reflex and negative angles?

1 Answers1