Problems with understanding rotor's conception

Question

By definition rotor is: $$ rot \vec A = \begin{bmatrix} (\frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z}) \\ (\frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x}) \\ (\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y}) \\ \end{bmatrix} $$

And I'm trying to visualize it. So if I have a vector field, take one vector, and find a projection, and I don't understand how we can take derivative on, for example for $\hat i$, $A_z$ if there is no y axis anymore (see pic.1) and for $A_y$ there is no z axis anymore

Answer 1

Take a point $(x,y,z)$. We can evaluate $\vec{A}(x,y,z)=(A_x,A_y,A_z)$ which is the vector of the vector field at $(x,y,z)$.

We may reinterpret this as being three separate functions $A_x,A_y$ and $A_z$, which take points of the space as input and give single numbers as output. As such, we can take partial derivatives of these three functions entirely without issue. These are probably the projections you talk about. Note that it is only the output that is projected. The input is still 3-dimensional.

Alternately, consider the partial derivatives of $\vec A$ itself. For instance, $$ \frac{\partial \vec A}{\partial x}=\lim_{h\to 0}\frac{\vec A(x+h,y,z)-\vec A(x,y,z)}{h} $$ which is the instantaneous change of $\vec A$ as you move in the $\vec i$ direction. Similarly with the two other partial derivatives. These three partial derivatives are vectors, and as such they each have $x,y$ and $z$ components.

Both these approaches give the same result. It is up to you which one you like best.

Answer 2

As an aside, while it is "ротор" in Russian (basically "rotor") and it's sometimes written $\mathop{\rm rot}\vec A$, this quantity would usually be called "curl" in English (and perhaps very occasionally "rotation" or "rotational", but probably never "rotor").

Your question was initially about curl, but it seems the main thing you are having trouble grasping is the meaning of a partial derivative of "the wrong" component, like $\dfrac{\partial A_x}{\partial y}$, where $\vec A=\left\langle A_x,A_y,A_z\right\rangle$.

It's important to keep in mind that for a particular piece of a vector field $\vec A$, there are not just three numbers to worry about ($A_x, A_y,A_z$), but actually $6$: the three inputs are important too. And things like partial derivatives and curl measure sensitivity to changes in input.

So we have something more like $\vec A(a,b,c)=\left\langle A_x,A_y,A_z\right\rangle=\left\langle A_x(a,b,c),A_y(a,b,c),A_z(a,b,c)\right\rangle$. $\dfrac{\partial A_x}{\partial y}$ then measures how much the $x$-component of the output changes with a small change to $b$, the $y$-component of the input. The $A_z$ displayed in the picture in the OP only shows the value of $A_z$ for a particular input $(a,b,c)$. And to approximate the derivative $\dfrac{\partial A_x}{\partial y}$, we need to look at both $(a,b,c)$ and $(a,b+h,c)$ for a small value of $h$.

We can look at this situation pictorially in this example:

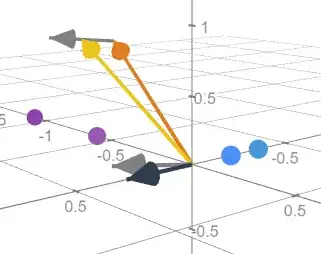
There are two vectors from a vector field $\vec A(x,y,z)$ floating off in space (not shown) positioned with tails at $(a,b,c)=(?,-1.1,?)$ and $(a,b+h,c)=(?,-1.1+0.5,?)=(?,-0.6,?)$. You can see the $y$-coordinates of the tails/inputs marked in purple on the $y$-axis.

Those vectors have been translated to have tails at the origin as orange and yellow vectors (with yellow corresponding to $\vec A(a,b+0.5,c)$). The $x$-coordinates of these outputs are displayed as blue points on the $x$-axis.

The difference quotient $\dfrac{\vec A(a,b+0.5,c)-\vec A(a,b,c)}{0.5}$ is displayed as a gray vector with its tail at the head of the orange vector (which corresponds to $\vec A(a,b,c)$). This grey vector is also translated to have its tail at the origin, representing an approximation to $\dfrac{\partial \vec A(x,y,z)}{\partial y}$ at $(a,b,c)$.

Finally, we look at the projection of this gray vector onto the $x$-axis to see the $x$ component: an approximation to $\dfrac{\partial \vec A_x(x,y,z)}{\partial y}$ at $(a,b,c)$.

You can vary the perspective, values, and function in this math3d interactive.