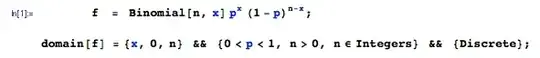The Fisher information is defined as $\mathbb{E}\Bigg( \frac{d \log f(p,x)}{dp} \Bigg)^2$, where $f(p,x)={{n}\choose{x}} p^x (1-p)^{n-x}$ for a Binomial distribution. The derivative of the log-likelihood function is $L'(p,x) = \frac{x}{p} - \frac{n-x}{1-p}$. Now, to get the Fisher infomation we need to square it and take the expectation.
First, we know, that $\mathbb{E}X^2$ for $X \sim Bin(n,p)$ is $ n^2p^2 +np(1-p)$. Let's first focus on on the content of the paratheses.
$$ \begin{align} \Bigg( \frac{x}{p} - \frac{n-x}{1-p} \Bigg)^2&=\frac{x^2-2nxp+n^2p^2}{p^2(1-p)^2} \end{align} $$
No mistake so far (I hope!).
\begin{align} \mathbb{E}\Bigg( \frac{x}{p} - \frac{n-x}{1-p} \Bigg)^2 &= \sum_{x=0}^n \Bigg( \frac{x}{p} - \frac{n-x}{1-p} \Bigg)^2 {{n}\choose{x}} p^x (1-p)^{n-x} \\ &=\sum_{x=0}^n \Bigg( \frac{x^2-2nxp+n^2p^2}{p^2(1-p)^2} \Bigg) {{n}\choose{x}} p^x (1-p)^{n-x} \\ &= \frac{n^2p^2+np(1-p)-2n^2p^2+n^2p^2}{p^2(1-p)^2}\\ &=\frac{n}{p(1-p)} \end{align}
The result should be $\frac{1}{p(1-p)} $ but I've been staring at this for a few hours incapable of getting a different answer. Please let me know whether I'm making any arithmetic mistakes.