Probability of getting a piece longer than $1/2$ on cutting a rope of length $1$ at two randomly chosen points

Question

Here's a bootstrap approach I used to find the answer (python 3).

def num_pieces(num,lenght):
    ot = list(range(1,lenght+1))[::-1]
    nig = []
    for i in range(lenght-1):
        n = random.randint(1, num-ot[i])
        nig.append(n)
        num -= n
    nig.append(num)
    r = []
    for i in nig:
         r.append(i/10)
    return r
res = []
n1 = 1000
n2 = int(n1/10)
for i in range(n1):
    a = []
    for i in range(n2):
        r = num_pieces(10,3)
        if r[0] > 0.5 or r[1] > 0.5 or r[2] > 0.5:
            a.append(1)
        else:
            a.append(0)
    res.append(sum(a)/n2)
pd.DataFrame(res).hist();

And here's the result

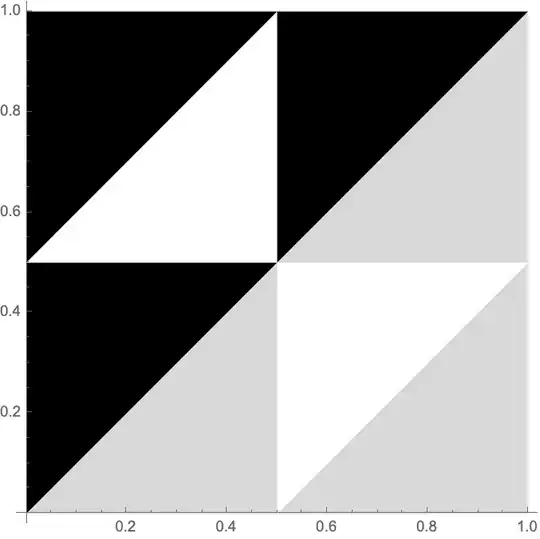
If my code is correct (I believe it is), the probability is about 50%

Question - I do not know how to solve this task using plain math. In other words - what is the math base under the bootstrap result?

UPDATE

After receiving those awesome answers below, I checked the code and fixed the num_pieces generator. It worked incorrectly. All other code works just fine. So, here's the final solution

def get_random():
    a = [random.random(), random.random()]
    c = 1 - (max(a))
    b = max(a) - min(a)
    a = min(a)
    return [a,b,c]
res = []
n1 = 1000
n2 = int(n1/10)
for i in range(n1):
    a = []
    for i in range(n2):
        r = get_random()
        if r[0] > 0.5 or r[1] > 0.5 or r[2] > 0.5:
            a.append(1)
        else:
            a.append(0)
    res.append(sum(a)/n2)
pd.DataFrame(res).hist();

The probability is 75% indeed. Thank you all for answering!

The second cut being made on the shorter piece is sufficient but not necessary for the longest piece to exceed 0.5m. For example, if the first cut divides the rope into 0.01m and 0.99m, the second cut is almost assured of producing one piece above 0.5m. — Greg Martin, Dec 28 '20 at 09:25

score 8 · Accepted Answer · answered Dec 28 '20 at 09:27

Think about it this way. Say $x$ is a number between $0$ and $1$, representing the position of the first cut. For instance, suppose $x = 0.25$. Now the second cut might occur on the short piece with probability $0.25$, and no matter where it is cut there, the long piece exceeds $0.5$. Or the long piece is cut with probability $0.75$, but if the second cut occurs too close to one of the ends of the long piece, the remaining length will still be greater than $0.5$; otherwise, if cut near the middle, the two pieces will be less than $0.5$. So we just have to figure out what we mean by being "too close" to one of the ends.

For the case $x = 0.25$, it is easy to see that if $y$ is the position of the second cut, if $0.25 < y < 0.5$, that is "too close" to an end--the remaining piece will be longer than $0.5$. And if $0.75 < y < 1$, then again, the second cut is too close to the other end, and the middle piece will be longer than $0.5$. So, given that $x = 0.25$, the probability that our second cut will give one section of rope that is longer than $0.5$ is the total length of all intervals satisfying $0 < y < 0.5$, or $0.75 < y < 1$; i.e., it is $0.5 + 0.25 = 0.75$.

Naturally, the next step is to generalize this to any choice of $x$. Without loss of generality, let $0 < x < 0.5$ (as the situation is symmetric about $x = 0.5$). Then as we saw above, every choice of $y$ between $0$ and $x$ will make the interval $[x, 1]$ longer than $0.5$, and every choice of $y$ between $x$ and $0.5$, or between $x + 0.5$ and $1$, will also make a segment longer than $0.5$. So the probability of the second cut occurring in the interval $[0, 0.5] \cup [x + 0.5, 1]$ is $1 - (x + 0.5) + (0.5 - 0) = 1 - x.$ That's a nice result!

Finally, we use calculus to integrate over all $x$ between $0$ and $0.5$, then multiply by $2$ because we need to account for symmetry. We have $$2 \int_{x=0}^{0.5} 1-x \, dx = \frac{3}{4}.$$ This is the desired probability.

It is worth noting that this problem is equivalent to asking for the probability that, if a stick of unit length is broken in two places, each selected independently and uniformly at random, the resulting pieces cannot be formed into a triangle. The reasoning shown in my answer is almost identical to what is described at the following link, which I found after writing my answer: https://www.themathdoctors.org/broken-sticks-triangles-and-probability-ii/ — heropup, Dec 28 '20 at 09:41
thank you so much for such a detailed answer!! Wish I had a teacher like you during my math classes in school) — Dmitri Ilin, Dec 28 '20 at 14:36

Greg Martin · Answer 2 · 2020-12-28T23:32:01.470

5

The answer is 75%. It can be evaluated via $$ 2 \int_0^1 \int_0^y \begin{cases} 1, &\text{if } \max\{x,y-x,1-y\} > \frac12 \\ 0, &\text{if } \max\{x,y-x,1-y\} \le \frac12 \end{cases} \bigg\} \,dx \,dy $$ (where we use symmetry to declare $x$ the left cut point and $y$ the right cut point).

In the graph below, the black triangles are the points $(x,y)$ from the integral above that satisfy $\max\{x,y-x,1-y\} > \frac12$ (and the light gray triangles are their symmetric twins $(y,x)$), while the white triangles are the points that satisfy $\max\{x,y-x,1-y\} \le \frac12$.

edited Dec 28 '20 at 23:32

answered Dec 28 '20 at 09:25

Greg Martin

78,820

2

I really like the graphical representation of the problem, but the colors could do with an explanation. – R.M. Dec 28 '20 at 17:35
Good point!—edited. – Greg Martin Dec 28 '20 at 23:32

score 4 · Answer 3 · answered Dec 28 '20 at 09:46

We have a piece of length $>{1\over2}$ iff (a) both cuts are on the same half of the rope, or (b) are on different halfs, but the right cut is further right on its half than the left cut on its half. The probability that one of these happens is ${1\over2}+{1\over2}\cdot{1\over2}={3\over4}$.

Probability of getting a piece longer than $1/2$ on cutting a rope of length $1$ at two randomly chosen points

UPDATE

3 Answers3