3

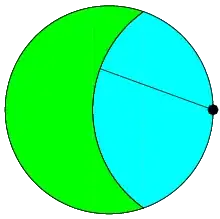
This year, there was published a closed-form solution to the Goat Problem. The problem seeks the radius of a circle (teal) with center on the edge of a unit circle (green) such that the first circle overlaps half of the unit circle.

Image from https://mathworld.wolfram.com/GoatProblem.html

The solution given is

$$r=2\cos\left(\frac{{\Large\oint}_{\large|z-3\pi/8|=\pi/4}{\Large\frac{z}{\sin{z}-z\cos{z}-\pi/2}}dz}{{\Large\oint}_{\large|z-3\pi/8|=\pi/4}{\Large\frac{2}{\sin{z}-z\cos{z}-\pi/2}}dz}\right)= 1.15872847\dots$$

Can we simplify this further? I noticed that the divided integrals look like a center of mass formula. I tried converting the contour integrals into real integrals, but didn't get very far. I don't have much experience with complex integration. Also, I don't have access to the paper, but maybe there is some information there that can help us.

tyobrien
  • 3,469
  • 4
    I wouldn't call that a "closed form", because you can evaluate the integrals only numerically. It's just residues the other way round, and you could write it with only one integral, obviously. –  Dec 27 '20 at 07:27

1 Answers1

-3

Yes, we can further simplify the closed solution to the Goat Problem:

I wrote an article about a simple and I think elegant solution to the Goat Problem several years ago. Here's a link to it:

https://www.keepandshare.com/doc6/41009/cow-goat-grazing-inside-a-circular-pasture-problem-pdf-513k?da=y

Bob Day
  • 1
  • Here is a MathJax tutorial. Also, try inserting the imgur link to the diagram. – Тyma Gaidash Oct 08 '23 at 21:53
  • 1
    Sorry, I'm confused about how this can be considered a closed-form solution. – Brian Tung Oct 14 '23 at 19:27
  • Is it closed form? I asked Google A I Bard about it. Bard seems to know what closed form is. I gave it the equation, and here's what it said: "Yes, the equation ∫(2r⋅cos−1(r/2))dr=π/2 is in closed form." And it followed that with a long and mathematically detailed explanation. – Bob Day Oct 28 '23 at 14:06