1

X and Y are independent and have the same exponential distribution wih density: $$\lambda e^{-\lambda x} 1_{(0,\infty)} (x) $$ The density of the X + Y distribution can be calculated by convolution of the functions: $$f*f(t)=\int_{-\infty}^{\infty} f(x) f(t-x) \, dx $$ but I still have no idea how to solve it, during the lecture we only gave an example for a uniform distribution on (0,1)

Michael Hardy
  • 1
Mia
  • 339
  • 1
    Have you plugged in $f(x) = \lambda e^{-\lambda x} 1_{(0,\infty)}(x)$ into the convolution integral? Where are you stuck? – angryavian Dec 27 '20 at 00:26

2 Answers2

2

Applying the convolution formula to your example you immediately get

$$f_Z(z)=\int_0^{z}\lambda e^{-\lambda x}\lambda e^{-\lambda (z-x)}dx=\lambda^2 z e^{-\lambda z}$$

$z\geq 0$

Proof:

By Definition you get

$$F_Z(z)=\int_{-\infty}^{\infty}f_X(x)\Bigg[\underbrace{\int_{-\infty}^{z-x}f_Y(y)dy}_{F_Y(z-x)}\Bigg]dx$$

Derivating you get the density

$$f_Z(z)=\frac{d}{dz}F_Z(z)=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)dx$$

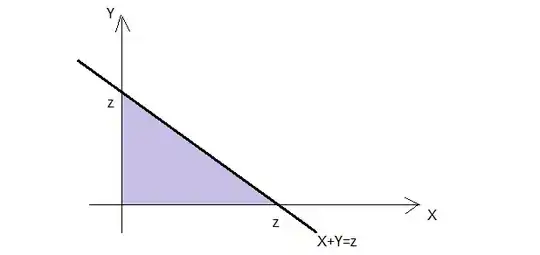
To realize that the integral bounds are $[0;z]$ just do a drawing of the transformation function

enter image description here

Without any calculations, $Z$ density could be found using the properties of Gamma distribution. As $Exp(\lambda)=Gamma(1;\lambda)$, thus $Z=X+Y\sim Gamma(2;\lambda)$

tommik
  • 32,733
  • 4
  • 15
  • 34
  • It appeared to me that what the original poster wanted was not a proof that convolution gives the answer, but a way to compute this particular convolution. – Michael Hardy Dec 27 '20 at 18:02
1

\begin{align} & \int_{-\infty}^\infty \lambda e^{-\lambda x} 1_{(0,\infty)} (x) \cdot \lambda e^{-\lambda (t-x)} 1_{(0,\infty)} (t-x) \, dx \\[12pt] = {} & \int_0^\infty \lambda e^{-\lambda x}(x) \cdot \lambda e^{-\lambda(t-x)} 1_{(0,\infty)}(t-x)\,dx \\ & \text{because } 1_{(0,\infty)}(x)=0 \text{ when } x<0 \\[12pt] = {} & \int_0^t \lambda e^{-\lambda x}(x) \cdot \lambda e^{-\lambda(t-x)} \,dx \\ & \text{because } 1_{(0,\infty)}(t-x)=0 \text{ when } x>t \\[12pt] = {} & \int_0^t \lambda^2 e^{-\lambda t} \,dx \end{align} and then observe that $\lambda^2 e^{-\lambda t}$ does not change as $x$ goes from $0$ to $t,$ i.e. you're integrating a constant function.

Michael Hardy
  • 1