Could not understand the physical meaning?

Question

Let's say a plane is defined using normal vector, i.e., $\vec{n_0}$ and a point, i.e., $p_0$ in the plane as shown in the above figure. So we can determine the corresponding equation of the plane as $ax+by+cz+d =0$ where $d = -p_0^T\vec{n_0}$

The following two expressions I count not understand what do they represent

1. $\frac{-\vec{n_0}\cdot d}{|\vec{n_0}|^2}$

2. Let assume there is another plane is given by ($\vec{n_1},p_1$), then compute $ \vec{n_1} \times \vec{n_0} \times \vec{n_1}$

These are I encounter when I try to understand how the reference plane intersects with a set of other planes. I could not share the original work due to copyright issue. Any idea on this to understand what actually those represent really appreciated.

Answer 1

1. $\dfrac{-\vec{n_0}}{\|\vec{n_0}\|}$ is the unit vector pointed in the opposite direction as $\vec{n_0}$. And $\dfrac d{\|\vec{n_0}\|}$ is the distance from the origin to the plane $\vec{n_0}\cdot \vec v = d$. Thus their product $$\dfrac{-d\vec{n_0}}{\|\vec{n_0}\|^2}$$ would be the vector pointing from the projection of the origin onto the plane back to the origin itself.
2. For any two non-parallel vectors $\vec v, \vec w$, $\vec v \times \vec w$ is a vector perpendicular to both, with length $\|\vec v\|\|\vec w\|\sin \theta$, where $\theta$ is the angle between the two. So
   • $\|\vec{n_1} \times \vec{n_0} \times \vec{n_1}\| = \|\vec n_0\|\|\vec n_1\|^2\sin \theta$.
   • $\vec{n_1} \times \vec{n_0} \times \vec{n_1}$ is perpendicular to $\vec{n_0} \times \vec{n_1}$, and therefore must be in the same plane as the origin, $\vec{n_0}$ and $\vec{n_1}$. It is also perpendicular to $\vec{n_1}$. Some playing around with the RH rule should also convince you that in the plane of $\vec{n_0}$ and $\vec{n_1}$, it lies on the same side of the line through $\vec{n_1}$ as $\vec{n_0}$. In fact, it is the projection of $\vec{n_0}$ onto the line perpendicular to $\vec{n_1}$ in the common plane of the two, multiplied by the the length of $\vec{n_1}$.

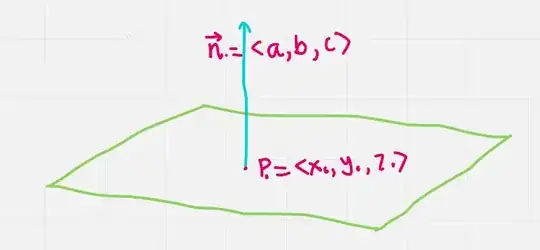
Note that in the equation of a plane $\vec n \cdot \vec r = D$, if we divide by the $\|\vec n\|$, we get $$\dfrac{\vec n}{\|\vec n\|}\cdot \vec r = \dfrac{D}{\|\vec n\|}$$ which is another equation of the same time, except that $\vec n$ is replaced with the vector $\dfrac{\vec n}{\|\vec n\|}$, which has length $1$, and the constant is replaced with another constant $\dfrac{D}{\|\vec n\|}$. That constant turns out to be exactly the distance from the plane to the origin, so it is more meaningful that $D$ itself.

For this reason we generally prefer to always write plane equations with the normal being a unit vector. And if we make that restriction the two interpretations become more simple. If $\vec{n_0}$ is a unit vector, then $d\vec{n_0}$ is the projection of the origin onto the plane. And $-d\vec{n_0}$ is its opposite.

When $\|\vec{n_0}\| = \|\vec{n_1}\| = 1$, then $\vec{n_1} \times \vec{n_0} \times \vec{n_1}$ is exactly the projection of $\vec{n_0}$ onto the line perpendicular to $\vec{n_1}$ in their common plane.