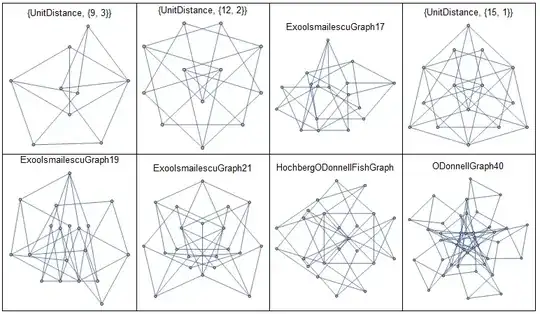
I've programmed the first seven graphs into my new Shibuya repository of unit-distance and integral embeddings of graphs. Strictly speaking I've only programmed six, but {UnitDistance, {15, 1}} contains {UnitDistance, {12, 2}} as a subgraph and the latter is (as will be shown) rigid, so the former is also rigid.
Using the same least-parameters method that I used to prove the rigidity of the braced heptagon, I get the following results. All the rigid graphs are first-order rigid:
| Graph |
Least parameters required |
Rigid? |
{UnitDistance, {9, 3}} |
1 |
yes |
{UnitDistance, {12, 2}} |
2 |
yes |
| Exoo–Ismailescu 17 |
2 |
yes |
| Exoo–Ismailescu 19 |
2+1 |
yes |
| Exoo–Ismailescu 21 |
2+1+1 |
no (1 DOF) |
| Hochberg–O'Donnell fish |
3+1+1 |
no (1 DOF) |
The notation $a+b+c+\cdots$ means that a subgraph was parametrised using $a$ parameters, then based on this another subgraph was parametrised using $b$ parameters and so on – the result of all these phases is the whole graph.
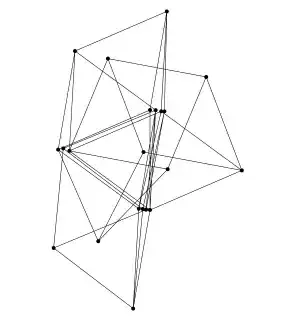
Exoo–Ismailescu 21 is not rigid because there are two parameters but only one constraint in the first phase; the second and third phases each have one parameter and one constraint, so they don't help with rigidity:
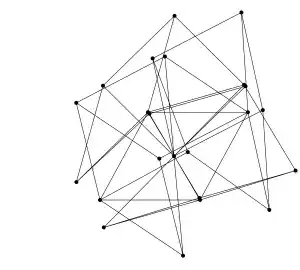
The reason for the "hodfish" graph not being rigid is similar, only the first phase has three parameters and two constraints:
You would have done well to check the number of edges of the two graphs shown to be non-rigid above. They fail the Laman condition (one fewer edge than $2v-3$ where $v$ is the number of vertices), which is necessary for a graph to be rigid.