This is a very interesting question.
EDIT 06.01.2021
Introducing what I call the equivalent 2x2-matrix appoach simplifies and unifies the task of finding $q(d)$ for all dimensions. The task now boils down to finding the order of an exponential congruence generalized to the 2x2 matrix.
EDIT 01.01.21
Explicit formulas for the mod(m) of $\alpha$ and $\beta$.
EDIT 30.12.20
Pursuing the second approach, in the case of even dimension $d$ we find a simple exponential congruence $\beta^k \equiv 1 \text{ mod(m)}$ ($\beta$ and $m$ are known integer functions of $d$) for which we need to find the smallest positive solution of the exponent $k$.
The general solution for this restricted case is still open (to me). Help from experts in number theory is greatly appreciated.
The more complicated case of odd $d$ has still to be done.
EDIT 27.12.20
Extension to two approaches to solve the generalized problem:
Brute force matrix multiplication (as in the original post)
Employing the characteristic polynom of the matrix and the Cayley-Hamilton theorem to derive a linear recurrence of the Fibonacci type
Generalized problem
Let $a(d)$ be a square matrix of dimension $d$ formed by consecutively filling in the numbers 1 through d^2 in lexicographic order.
The elements are hence
$$a_{ik}=i+d(k-1)\tag{1}$$
Now form the set $s(d) = (a, a^2, a^3, ..., a^q)$ of consecutive powers of the matrix $a$ taken modulo $m=d^2+1$, which we designate by $[..]$. The power $q$ is defined by the maximum value of $q$ for which all elements in the set $s(q)$ are different.
Task: find $q(d)$
Solution
0) Equivalent 2x2 matrix
This approach is a compact formulation of the results of my earlier studies documented before in this answer. It is valid for all dimensions $d$ and is based on the following theorem 1 which I provide here for the moment without proof.
Theorem 1
Consider the matrix
$$A(d) = \begin{bmatrix}\alpha(d) & 1 \\ \beta(d)&0 \end{bmatrix}\tag{0.1}$$
where
$$\alpha(d) = \frac{1}{2} d(d^2+1)\tag{0.2a}$$
$$\beta(d) = \frac{1}{12}d^3(d^2-1)\tag{0.2b}$$
and let
$$m=1+d^2\tag{0.3}$$
Then the number $q(d)$ of different powers of the original matrix $a$ of the OP defined in $(1)$ is given for $d$ even by the order $k$, and for $d$ odd by $k+1$ in the exponential congruence
$$A^{k+1} \equiv A \text{ (mod m)}\tag{0.4}$$
where the action of the module function on a matrix is defined as the action on its elements. Generalizing slightly the terminology of exponential congruences the order of a matrix $A$ modulo $m$ is defined as the smallest number $k>0$ for which $(0.4)$ holds.
1) Brute force calculation of the powers of the matrix of the OP
Let us start small.
For $d=2$ the first 9 powers of
$$a = \begin{bmatrix}1 & 2 \\ 3&4 \end{bmatrix}$$
mod 5 are
$$
\begin{array}{cc}
a = \begin{bmatrix}1 & 2 \\ 3&4 \end{bmatrix},
[a^2] = \begin{bmatrix}2 & 0 \\ 0&2 \end{bmatrix},
[a^3] = \begin{bmatrix}2 & 4 \\ 1&3 \end{bmatrix},
[a^4] = \begin{bmatrix}4 & 0 \\ 0&4 \end{bmatrix},\\
[a^5] = \begin{bmatrix}4 & 3 \\ 2&1 \end{bmatrix},
[a^6] = \begin{bmatrix}3 & 0 \\ 0&3 \end{bmatrix},
[a^7] = \begin{bmatrix}3 & 1 \\ 4&2 \end{bmatrix},\\
[a^8] = \begin{bmatrix}1 & 0 \\ 0&1 \end{bmatrix},
[a^9] = \begin{bmatrix}1 & 2 \\ 3&4 \end{bmatrix}
\end{array}
\tag{2}$$
We see that $[a^9] = a$ so that $q(2)=8$.
For $d=3$, the case of the OP, we have
$$
\begin{array}{ccc}
a= \begin{bmatrix}1 & 2&3 \\ 4&5&6\\7&8&9 \end{bmatrix},
[a^2] = \begin{bmatrix}0 & 6&2 \\ 6&1&6\\2&6&0 \end{bmatrix},
[a^3] = \begin{bmatrix}8&6&4 \\ 2&5&8\\6&4&2 \end{bmatrix},\\
[a^4] = \begin{bmatrix}0&8&6 \\ 8&3&8\\6&8&0 \end{bmatrix},
[a^5] = \begin{bmatrix}4&8&2 \\ 6&5&4\\8&2&6 \end{bmatrix},
[a^6] = \begin{bmatrix}0&4&8\\9&4&9\\8&4&0 \end{bmatrix},\\
[a^7] = \begin{bmatrix}2&4&6\\8&5&2\\4&6&8\end{bmatrix},
[a^8] = \begin{bmatrix}0&2&4\\2&7&2\\4&2&0\end{bmatrix},
[a^9] = \begin{bmatrix}6&2&8\\4&5&6\\2&8&4\end{bmatrix},\\
[a^{10}] = \begin{bmatrix}0&6&2\\6&1&6\\2&6&0\end{bmatrix}
\end{array}
\tag{3}$$
Interestingly, for $d=3$, the case of the OP, there is no power $k\gt 1$ for which $[a^k] = a$ but we have $[a^{10}] = [a^2]$, hence $q(3)=9$.
Now we let mathematica work out the first 20 values of $q(d)$:
$$q(d) =\\ \{1,8,9,32,7,2,41,24,81,40,\\31,56,33,56,225,512,57,120,61,800\}\tag{4}$$
2) Employing the characteristic polynomial of the matrix and reducig the problem to a linear recurrence relation of second order
The characteristic polynomial of a matrix $A$ is defined by
$$p(A,\lambda) = \left| \lambda I - A\right|\tag{5}$$
and the characteristic equation $p(A,\lambda)=0$ gives the eigenvalues $\lambda$ of $A$ as roots.
For our matrix $a$ defined by $(1)$ the list of the first ten polynomials for $d=1..10$ in the format $\{d,p\}$ is
$$
\begin{array}{c}
\{1,\lambda -1\} \\
\left\{2,\lambda ^2-5 \lambda -2\right\} \\
\left\{3,\lambda ^3-15 \lambda ^2-18 \lambda \right\} \\
\left\{4,\lambda ^4-34 \lambda ^3-80 \lambda ^2\right\} \\
\left\{5,\lambda ^5-65 \lambda ^4-250 \lambda ^3\right\} \\
\left\{6,\lambda ^6-111 \lambda ^5-630 \lambda ^4\right\} \\
\left\{7,\lambda ^7-175 \lambda ^6-1372 \lambda ^5\right\} \\
\left\{8,\lambda ^8-260 \lambda ^7-2688 \lambda ^6\right\} \\
\left\{9,\lambda ^9-369 \lambda ^8-4860 \lambda ^7\right\} \\
\left\{10,\lambda ^{10}-505 \lambda ^9-8250 \lambda ^8\right\} \\
\end{array}
\tag{6}$$
The general form of $p(a,d)$ can be written as
$$p(a,d) = \lambda ^d-\alpha ( d) \lambda ^{d-1}-\beta ( d) \lambda ^{d-2}\tag{7}$$
where
$$\alpha (d)=\frac{1}{2} d \left(d^2+1\right)\tag{8a}$$
$$\beta (d)=\frac{1}{12} d^3 \left(d^2-1\right)\tag{8b}$$
Now the theorem of Cayley and Hamilton states that a matrix obeys its own characteristic equation.
For example from $(6$) we get for $d=2$ the equation
$$a^2 = 5a + 2\tag{9}$$
where we have dropped writing down the unit matrix $I$.
This equation allows to write higher powers of $a$ in terms of a linear combination of lower powers. Indeed, if we also take into account that all terms should be taken mod $d^2+1=5$ for $d=2$, the elements of the set $s$ are can be calculated as follows
$$a, \\a^2 \to 5a+2\equiv 2 \text{ (mod 5)}, \\a^3=5a^2+2a \equiv_{5} 2a \\a^4 = 2a^2\to 2\times 2= 4\\a^5 = 4a\\a^6 \equiv_{5} 4a^2\to 4 \times 2 = 8\equiv_{5} 3\\a^7=3a\\ a^8 = 3a^2 \to 3 \times 2 = 6 \equiv_{5} 1 $$
Hence
$$s(d=2) = \{a, 2, 2a, 4, 4a, 3, 3a, 1\}$$
which has $8$ different elements, hence $q(2)=8$.
The generalization is not difficult. We have to employ $(7)$ to get the general power of $a$.
We are going to do this by solving the corresponding difference equation
$$c_{k} = \alpha c_{k-1} + \beta c_{k-2}\tag{10}$$
with the initial conditions
$$c_1 = a, c_2 = a^2\tag{11}$$
$(10)$ is a linear difference equation of the Fibonacci type which can be easily solved by standard methods.
The result is with two constants $u$ and $v$
$$c(k) = u \; . 2^{-k} \left(\alpha -\sqrt{\alpha ^2+4 \beta }\right)^k\\+v\;. 2^{-k} \left(\alpha +\sqrt{\alpha^2+4 \beta }\right)^k\tag{12} $$
Modular arithmetic
We pause here for a moment to study the modular arithmetic of the function $\alpha(d)$ and $\beta(d)$, i.e. their remainder mod $m=(1+d^2)$.
For $\alpha$ we have
$$\alpha(d \text{ even})\equiv 0\tag{13a}$$
$$\alpha(d \text{ odd})\equiv_{m} \frac{1}{2}(1+d^2)\tag{13b}$$
For $\beta$ things are more complicated.
The first few terms for $\beta(d)$ mod($m$) are
$$ \beta(d) |_{d=1}^{d=20} \equiv_{m} \\ \{0, 2, 8, 12, 16, 1, 22, 23, 22, 69, 12, 2, 158, 68, 172, 174, 172, 3, 154, 137\}\tag{14a}$$
We can analyse the structure of this sequence by plotting it.
For even d we get
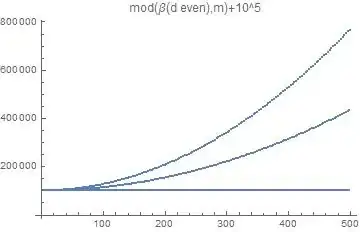
and for odd d
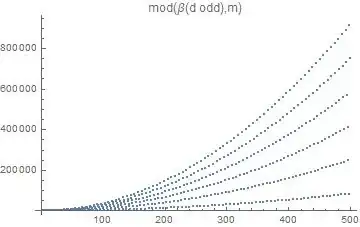
We see that there are "hidden" sub-sequences.
Specifically, three and six sub-sequences for even and odd d, respectively.
Closer inspection shows that we have explicit formulas for the sequences as follows
$\beta(d \text{ even))}\equiv_{m}
\left\{
\begin{array}{ll}
\frac{d}{6} & \;\; d \equiv_{6} 0\\
12 \left(\frac{d-2}{6}\right)^2+\frac{9 (d-2)}{6}+2 & \;\; d \equiv_{6} 2\\
24 \left(\frac{d-4}{6}\right)^2+\frac{33 (d-4)}{6}+12 & \;\; d \equiv_{6} 4\\
\end{array}
\right. \tag{14b}$
$\beta(d \text{ odd))}\equiv_{m}
\left\{
\begin{array}{ll}
132 \left(\frac{d-1}{12}\right)^2+\frac{24 (d-1)}{12}+2 & \;\; d \equiv_{12} 1\\
108 \left(\frac{d-3}{12}\right)^2+\frac{56 (d-3)}{12}+8 & \;\; d \equiv_{12} 3\\
84 \left(\frac{d+7}{12}\right)^2-\frac{96 (d+7)}{12}+28 & \;\; d \equiv_{12} 5\\
60 \left(\frac{d+5}{12}\right)^2-\frac{48 (d+5)}{12}+10 & \;\; d \equiv_{12} 7\\
36 \left(\frac{d+3}{12}\right)^2-\frac{16 (d+3)}{12}+2 & \;\; d \equiv_{12} 9\\
12 \left(\frac{d+1}{12}\right)^2 & \;\; d \equiv_{12} 11\\
\end{array}
\right. \tag{14c}$
Now that we have explicit formulas for the mod(m) of $\alpha$ and $\beta$ we can dive deeper.
Let us start with the case of even $d$ where $\alpha\equiv_{m}=0$ and the characteristic equation is simply
$$a^3 = \beta(d) a\tag{15}$$
(to do: the next steps have to be revised in view of $(14b)$ and $(14c)$).
Explicitly the first 10 equations are in the format {d, m, equn} are
$$
\begin{array}{c}
\left\{2,5,a^3\equiv 2 a\right\} \\
\left\{4,17,a^3\equiv 12 a\right\} \\
\left\{6,37,a^3\equiv a\right\} \\
\left\{8,65,a^3\equiv 23 a\right\} \\
\left\{10,101,a^3\equiv 69 a\right\} \\
\left\{12,145,a^3\equiv 2 a\right\} \\
\left\{14,197,a^3\equiv 68 a\right\} \\
\left\{16,257,a^3\equiv 174 a\right\} \\
\left\{18,325,a^3\equiv 3 a\right\} \\
\left\{20,401,a^3\equiv 137 a\right\} \\
\end{array}
\tag{16}$$
All sets $s$ start with $\{a,a^2,a^3\}$. Now $a^3$ has to be replaced from the corresponding by $\beta(d) a$, the next element is $\beta a^2$, and so on.
Hence
$$s = \{a,a^2, \beta a, \beta a^2, \beta^2 a, \beta^2 a^2, ...,\beta^k a, \beta^k a^2 \}\tag{17} $$
The last two elements of s are a repetition of the first two if
$$\beta(d \text{ even})^k \equiv 1 \text{ mod}(m)\tag{18a}$$
Remember that $m=1+d^2$ and that $\beta$ is given by $(8b)$.
Let $k_{min}$ be the smallest positive value which solves $(18a)$. The number $k_{min}$ is called the order of $\beta$ modulo $m$. Then the number of elements of the set s is given by
$$q(d) = |s| = 2 k_{min}\tag{18b}$$
Our task is hence reduced for even $d$ to the problem of finding the order of $\beta(d)$ modulo $1+d^2$.
Concerning its general solution we have to look up the theory of exponential congruences. Nice examples are Solution to exponential congruence and https://www.youtube.com/watch?v=oCgWwB465p8.
However, an upper limit of $k$ can be found using the little Fermat theorem in the formuation of Euler which states that if $m$ and $\beta$ have no common divisors (which is the case in our examples) then
$$k = k_{\phi} = \phi(m)\tag{19}$$
solves $(18a)$. Here $\phi(m)$ is Euler's totient function. Unfortunately, in most cases $k_{\phi}$ is not the smallest solution of $(18a)$.
Indeed, for d=8 we have m=65, $\beta=23$, $\phi(65) = 48$ but we have already $23^{12}\equiv 1 \text{ mod 65}$
It is helpful to notice that the order of $\beta$ modulo $m$ must be a divisor of $\phi(m)$. Hence we have reduced the possible number of orders. In the case of prime $m$ we have $\phi(m) = m-1=d^2$.
An even more effective procedure to find the order is described here https://math.stackexchange.com/a/165728/198592.
Discussion
For the specific problem of the OP which has $d=3$ the answer is 9. There are 9 different matrices.
Two values appear twice ($q(12)=q(14)=56$.
The case $d=6$ is remarkable since here already $[a^3] = a$
I have not found a general formula for $q(d)$. This might be difficult since the sequence is not contained in https://oeis.org/.
Matrix multiplication and taking the module
We can verify that for two matrices $a$ and $b$ with integer elements we have the relation
$$[ a.b ] = [[a].[b]]\tag{5}$$
Hence the two operations can be interchanged.
Group properties?
The set $s$ does not form a group for the simple reason that the matrix $a$ is singular and hence has no inverse.
The even powers have an inverse but in general have non integer elements, and also do not generate a unit element.
Rather, for each $d$, the set $s$ is an algebra with a multiplication rule defined by the characteristic equation.

