I don't know how to prove the generalized continued fraction $\pi/2=[1;1/1,1/2,1/3,1/4,...]=1+\cfrac{1}{1/1+\cfrac{1}{1/2+\cfrac{1}{1/3+\cfrac{1}{1/4+\ddots}}}}$
It appears on wikipedia without proof, it contains the terms of the harmonic series but it seems not to be very well known.
I would appreciate any help, thanks.
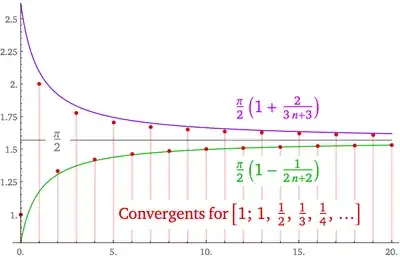
The article shows that as the harmonic series $\sum\frac{1}{n}$ diverges, one can apply Van Vleck's theorem to show that the $2n$th and $(2n+1)$th convergents of the continued fraction $[1; 1, 1/2, 1/3,\dots]$ both exist and converge to the same limit.
The author transforms $[1;1,1/2,1/3,\dots]$ into the form $$1+\frac{1\cdot1}{1+\frac{1\cdot2}{1+\frac{2\cdot3}{1+\dots}}}$$ by multiplying the numberator and the denominator of the $n$th fraction by $n$. Let $f_n$ be the numerator or the denominator of the $n$th (even) convergent then $f_n$ satisfies the relation $$f_n=(2n^2-4n+3)f_{n-2}-(n-1)(n-2)^2(n-3)f_{n-4}$$ By direct substitutions, one can show that $A_n$ and $B_n$ where $A_n=\prod_{k\text{ even}}^nk^2$ and $B_n=(n+1)\prod_{k\text{ odd}}^{n-1}k^2$ satisfy the relation for even $n$s. The fraction $\frac{A_n}{B_n}$ has a limit known as the Wallis product. Since for odd $n$s the $n$th convergent converges to the same limit as previously proved, the continued fraction converges to $\frac{\pi}{2}$.
I hope this is a clear summary of the article that can save you some time. Sorry for falsely flagging your question.
Edit:
(1) If you are not familiar with the Van Vleck theorem, it is helpful to study the Seidel-Stern theorem. This theorem states that if $\sum b_n=\infty$ and $b_n$ positive, then $K(1/b_n)$ (the continued fraction) converges. The proof of this theorem can be found in Waadeland and Lorentzen's text Continued Fractions with Applications, Chapter 3 Theorem 3. The proof takes advantage of the fact that $$\frac{A_{2n+1}}{B_{2n+1}}-\frac{A_{2n}}{B_{2n}}=\frac{1}{B_{2n}B_{2n+1}}\to 0$$ as $n\to\infty$. This can be seen from the recursive relation $$B_{n}=b_nB_{n-1}+B_{n-2}$$ Since the $b_n$ are positive, we have $B_{2n}>B_{2n-2}>\cdots>B_0=1$ and $B_{2n+1}>\cdots>B_1=b_1$. Therefore $$B_{2n}>b_{2n}b_1+B_{2n-1}>\cdots>(b_{2n}+b_{2n-2}+\cdots+b_2)b_1+1$$ and $$B_{2n+1}>b_{2n+1}+B_{2n-1}>\cdots>b_{2n+1}+b_{2n-1}+\cdots+b_1$$ Since $\sum b_n$ divergese, the denominator goes to infinity with $n$.
Van Vleck's theorem, on the other hand, concerns the convergence of the continued fraction $K(a_n/b_n)$ with complex $a_n, b_n$. It gives a more general criterion for convergence according to the argument of $b_n$ and the divergence of $\sum |b_n|$ (in our case the argument is zero and $|b_n|=b_n$).
(2) The recursive relation is in no way magical. Let $f_n$ be the denominator or the numerator of the $n$th convergent, we have $$f_n=b_nf_{n-1}+a_nf_{n-2}$$ $$f_{n-1}=b_{n-1}f_{n-2}+a_{n-1}f_{n-3}$$ $$f_{n-2}=b_{n-2}f_{n-3}+a_{n-2}f_{n-4}$$ like any continued fraction. Then $f_{n-3}=1/b_{n-2}(f_{n-2}-a_{n-2}f_{n-4})$. Plugging the second relation into the first one, one gets $$f_n=(b_{n}b_{n-1}+a_n+a_{n-1}b_n/b_{n-2})f_{n-2}-a_{n-1}a_{n-2}b_n/b_{n-2}f_{n-4}$$
After the transformation we did, $b_i=1$ for all $i$ and $a_n=n(n-1)$ for $n>1$. Thus, $$\begin{aligned} f_n &=(1+n(n-1)+(n-2)(n-1))f_{n-2}-(n-1)(n-2)^2(n-3)f_{n-4}\\ &=(2n^2-4n+3)f_{n-2}-(n-1)(n-2)^2(n-3)f_{n-4} \end{aligned}$$
References:
Lorentzen, L. and Waadeland, H. (1992). Continued fractions with applications. Amsterdam ; London ; New York ; Tokyo: Elsevier Science Publishers B. V.
Pickett, T.J. and Coleman, A. (2008). Another Continued Fraction for π. The American Mathematical Monthly, 115(10), pp.930–933.
Matrix Representation of Convergents
One method to compute the convervgents of continued fractions uses matrices: if $[c_0;c_1,c_2,\dots,c_n]=\frac{p_n}{q_n}$, then $$ \begin{bmatrix}0&1\\1&0\end{bmatrix} \prod_{k=0}^n\begin{bmatrix}0&1\\1&c_k\end{bmatrix} =\begin{bmatrix}p_{n-1}&p_n\\q_{n-1}&q_n\end{bmatrix}\tag1 $$ Since $c_0=1$, and for $k\ge1$, $c_k=\frac1k$ we get $$ \begin{bmatrix}1&1\\0&1\end{bmatrix} \prod_{k=1}^n\begin{bmatrix}0&1\\1&\frac1k\end{bmatrix} =\begin{bmatrix}p_{n-1}&p_n\\q_{n-1}&q_n\end{bmatrix}\tag2 $$
Closed Form
We will show by induction that $$ \begin{bmatrix}1&1\\0&1\end{bmatrix} \prod_{k=1}^{2n}\begin{bmatrix}0&1\\1&\frac1k\end{bmatrix} =\begin{bmatrix} \frac{4^n}{\binom{2n}{n}}&\frac{4^n}{\binom{2n}{n}}\\ \frac{\binom{2n}{n}2n}{4^n}&\frac{\binom{2n}{n}(2n+1)}{4^n} \end{bmatrix}\tag3 $$ Note that $(3)$ is true for $n=0$. Assume $(3)$ is true for some $n$, then $$ \begin{bmatrix} \color{#C00}{\frac{4^n}{\binom{2n}{n}}}&\color{#C00}{\frac{4^n}{\binom{2n}{n}}}\\ \color{#090}{\frac{\binom{2n}{n}2n}{4^n}}&\color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}} \end{bmatrix} \begin{bmatrix} 0&1\\1&\frac1{2n+1} \end{bmatrix} =\begin{bmatrix} \frac{4^n}{\binom{2n}{n}}&\color{#C00}{\frac{4^{n+1}}{\binom{2n+2}{n+1}}}\\ \frac{\binom{2n}{n}(2n+1)}{4^n}&\color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}} \end{bmatrix}\tag4 $$ The left column of the result is easy, the right column top element is $$ \begin{align} \color{#C00}{\frac{4^n}{\binom{2n}{n}}}\cdot1+\color{#C00}{\frac{4^n}{\binom{2n}{n}}}\cdot\frac1{2n+1} &=\frac{4^n}{\binom{2n}{n}}\frac{2n+2}{2n+1}\tag{5a}\\ &=\frac{4^n}{\binom{2n}{n}}\frac{(2n+2)^2}{(2n+1)(2n+2)}\tag{5b}\\ &=\color{#C00}{\frac{4^{n+1}}{\binom{2n+2}{n+1}}}\tag{5c} \end{align} $$ the right column bottom element is $$ \begin{align} \color{#090}{\frac{\binom{2n}{n}2n}{4^n}}\cdot1+\color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}}\cdot\frac1{2n+1} &=\color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}}\tag6 \end{align} $$ We can continue $$ \begin{bmatrix} \color{#C00}{\frac{4^n}{\binom{2n}{n}}}&\color{#C00}{\frac{4^{n+1}}{\binom{2n+2}{n+1}}}\\ \color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}}&\color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}} \end{bmatrix} \begin{bmatrix} 0&1\\1&\frac1{2n+2} \end{bmatrix} =\begin{bmatrix} \frac{4^{n+1}}{\binom{2n+2}{n+1}}&\color{#C00}{\frac{4^{n+1}}{\binom{2n+2}{n+1}}}\\ \frac{\binom{2n}{n}(2n+1)}{4^n}&\color{#090}{\frac{\binom{2n+2}{n+1}(2n+3)}{4^{n+1}}} \end{bmatrix}\tag7 $$ The left column of the result is easy, the right column top element is $$ \begin{align} \color{#C00}{\frac{4^n}{\binom{2n}{n}}}\cdot1+\color{#C00}{\frac{4^{n+1}}{\binom{2n+2}{n+1}}}\cdot\frac1{2n+2} &=\frac{4^n}{\binom{2n}{n}}+\frac{4^n}{\binom{2n}{n}}\frac4{\frac{(2n+1)(2n+2)^2}{(n+1)^2}}\tag{8a}\\ &=\frac{4^n}{\binom{2n}{n}}+\frac{4^n}{\binom{2n}{n}}\frac1{2n+1}\tag{8b}\\ &=\frac{4^n}{\binom{2n}{n}}\frac1{\frac{(2n+1)(2n+2)}{(2n+2)^2}}\tag{8c}\\ &=\color{#C00}{\frac{4^{n+1}}{\binom{2n+2}{n+1}}}\tag{8d} \end{align} $$ the right column bottom element is $$ \begin{align} \color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}}\cdot1+\color{#090}{\frac{\binom{2n}{n}(2n+1)}{4^n}}\cdot\frac1{2n+2} &=\frac{\binom{2n}{n}(2n+1)}{4^n}\frac{(2n+2)(2n+3)}{(2n+2)^2}\tag{9a}\\ &=\color{#090}{\frac{\binom{2n+2}{n+1}(2n+3)}{4^{n+1}}}\tag{9b} \end{align} $$ $(4)$ and $(7)$ show that $(3)$ is true for $n+1$.
Estimating the Convergents
$(1)$ and $(3)$ show that
$$
\frac{p_{2n-1}}{q_{2n-1}}=\frac1{2n}\left(\frac{4^n}{\binom{2n}{n}}\right)^2\tag{10}
$$
$$
\frac{p_{2n}}{q_{2n}}=\frac1{2n+1}\left(\frac{4^n}{\binom{2n}{n}}\right)^2\tag{11}
$$
$(10)$ and $(11)$ can be unified as
$$
\frac{p_n}{q_n}=\frac1{n+1}\left(\frac{4^{\lceil n/2\rceil}}{\binom{2\lceil n/2\rceil}{\lceil n/2\rceil}}\right)^2\tag{12}
$$
$(10)$ from this answer says that
$$
\pi\left(n+\tfrac14\right)\le\left(\frac{4^n}{\binom{2n}{n}}\right)^2\le\pi\left(n+\tfrac13\right)\tag{13}
$$
Since $\frac n2\le\lceil n/2\rceil\le\frac{n+1}2$, $(12)$ and $(13)$ show that
$$
\frac\pi2\left(1-\frac1{2n+2}\right)\le\frac{p_n}{q_n}\le\frac\pi2\left(1+\frac2{3n+3}\right)\tag{14}
$$
which, by the Squeeze Theorem, says that
$$
\bbox[5px,border:2px solid #C0A000]{\lim_{n\to\infty}\left[1;1,\tfrac12,\tfrac13,\dots,\tfrac1n\right]=\frac\pi2}\tag{15}
$$
Wallis Product
The Wallis Product for $\pi$ is $$ \frac\pi2=\prod_{k=1}^\infty\frac{4k^2}{4k^2-1}\tag{16} $$ Consider the partial products $$ \begin{align} \prod_{k=1}^n\frac{4k^2}{4k^2-1} &=\prod_{k=1}^n\frac{2k}{2k+1}\frac{2k}{2k-1}\tag{17a}\\ &=\prod_{k=1}^n\frac{2k-1}{2k+1}\left(\frac{2k}{2k-1}\right)^2\tag{17b}\\ &=\frac1{2n+1}\left(\prod_{k=1}^n\frac{(2k)^2}{(2k-1)2k}\right)^2\tag{17c}\\ &=\frac1{2n+1}\left(\frac{4^n}{\binom{2n}{n}}\right)^2\tag{17d} \end{align} $$ Note the similarity between $(11)$ and $\text{(17d)}$.
