0

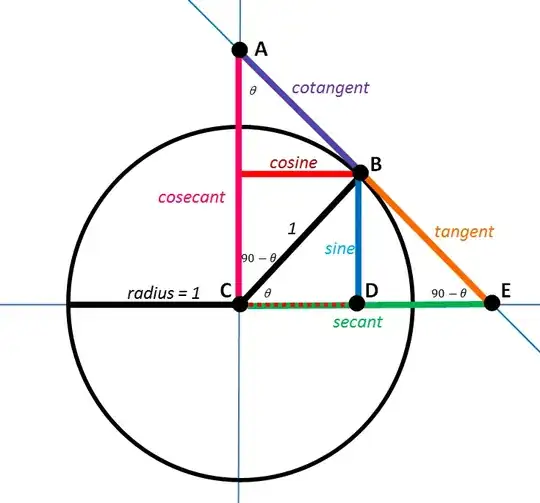
Arrange in ascending order $\tan45^\circ,\tan80^\circ$ and $\tan100^\circ.$

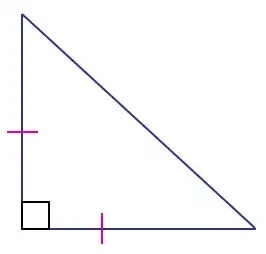
We know that $\tan45^\circ=1$ because a right triangle with angle equal to $45^\circ$ is isosceles. enter image description here

I don't know the exact values of $\tan80^\circ$ and $\tan 100^\circ.$ Can you give me a hint?

Math Student
  • 2,656

3 Answers3

1

Hint:

$\tan x \lt 0$ for $90^\circ\lt x \lt 180^\circ$ and $\tan x$ is an increasing function on $[0,90^\circ)$.

enter image description here

$\tan \theta$ is defined to be the orange line in the diagram. What happens to this line as $\theta$ goes from $0^\circ$ to $90^\circ$?

Vishu
  • 14,469
1

Write $\tan=\dfrac{\sin}{\cos}$

$$\tan80^\circ-\tan45^\circ=\cdots=\dfrac{\sin(80-45)^\circ }{\cos80^\circ\cos45^\circ}>0$$

We know $\tan45^\circ=?$

and $\tan100^\circ=\tan(180^\circ-80^\circ)=-\tan80^\circ<0$

lab bhattacharjee
  • 274,582
  • Thank you for the response! I am on $\tan80^\circ-\tan45^\circ=\dfrac{\sin80^\circ\cos45^\circ-\sin45^\circ\cos80^\circ}{\cos80^\circ\cos45^\circ}$. Why is that equal to $\dfrac{\sin(80-45)^\circ }{\cos80^\circ\cos45^\circ}?$ – Math Student Dec 20 '20 at 18:27
  • 1
    @nicoledobreva, https://math.stackexchange.com/questions/705021/trigonometry-identity-prove-that-sina-b-sin-a-cos-b-cos-a-sin-b – lab bhattacharjee Dec 20 '20 at 18:31
  • 1
    Thank you! We are using the trig identity: $\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta.$ We haven't studied it and the proof does not seem easy. So we have $\tan80^\circ-\tan45^\circ=\dfrac{\sin35^\circ}{\cos80^\circ\cos45^\circ}>0,$ right? Therefore, $\tan80^\circ>\tan45^\circ.$ – Math Student Dec 20 '20 at 18:50
1

$\tan(x)$ is defined on $\bigcup_{n\in \Bbb Z} (90(2n-1), 90(2n+1))$ (when working in degrees) and increasing inside each such set.

Moreover, recall that $\tan(x)\equiv\tan(x+180k)$ for each $k\in \Bbb Z$

So, we may say that $\tan(x)$ is increasing on the range $(-90, 90)$, as seen when $n=0$, and $\tan(100)=\tan(-80)<\tan(45)<\tan(80)$

Rhys Hughes
  • 12,842