A theoretical model of a flow network.

Question

I believe I've got a correct understanding of how flow network works.

Yet, I've bumped into a theoretical question that I'm not even sure if interpreted right. Here it is:

Provide an example of a network with n nodes and with integer capacities such that there is an exponential (i.e. greater than $c^n$ for some constant $c \gt 1$) number of different integer maximal flows in it. Two flows are considered different if they differ on at least one arc of the network

Unfortunately, I cannot post picture of a graph that I've constructed (due to the lack of 10 reputation), so I'll describe it formally

$V = \lbrace S, 1, 2, 3, T\rbrace$ $C(S,1) = s1$

$C(S,2) = s2$

$C(S,3) = s3$

$C(T,1) = t1$

$C(T,2) = t2$

$C(T,3) = t3$

$C(1,2) = ?$

$C(S,1) = ?$

So, one thing that I understood about that excercise, is that in order to have sufficient input flow and output capacity $$t1 + t2 + t3 \ge c^n \le s1 + s2 + s3$$

But what about $C(1,2)$ and $C(2,3)$? Maybe I've got totally wrong idea about question itself?

It would be a huge help even to paraphrase the task, as I think I'm reading it wrong.

Answer 1

Since you want to have exponentially many maximal flows, one way to construct it is to give many choice at first then to make a bottleneck.

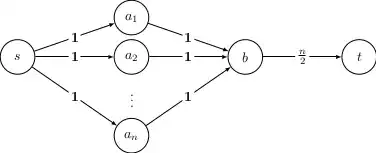
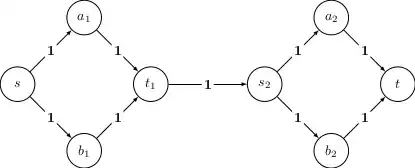
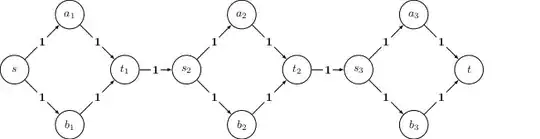As the original question asked to construct a graph for an arbitrary $n$, we will give a whole family of graphs $(G_n)_n$ with $G_n$ having (roughly) $n$ vertices and around $2^n$ different maximal flows(the graphs will actually have $n+1$ vertices plus the source and the sink, but it doesn't matter for the asymptotic):

Le $G_n$ be the following graph :

its quite clear that a maximal flow has a capacity of $n \over 2$, now, one as to chose which vertices $a_i$ to visit for the flow. Clearly there is $\binom{n}{n/2}$ possible choice, meaning that there are $\binom{n}{n/2}$ different maximal flows. The asymptotics of this number is $2^n$ (see limit of $2n$-th root of $2n$-th central binomial coefficient -- $\lim_{n\to \infty}{2n \choose n}^{\frac{1}{2n}}$ for instance)

You can get more precise estimate on the number of flows but I hope this is more or less what you've asked.

[EDIT] rethinking about it, this construction is a bit of an overkill as we can find an answer that does not involve knowing the asymptotic of the binomial coefficient (we'll end up with a smaller constant $c$ though).

the following graph

has graph with $8=2\times 4$ vertices and $4=2^2$ maximal flows.

Using three times this diamond shaped graph we end up with : $3\times 4$ vertices and $2^3$ maximal flows" /> which has $12=3\times 4$ vertices and $8=2^3$ maximal flows

Repeating $k$ times this diamond shaped graph give a graph with $4k$ vertices and $2^k$ maximal flows, so $n= 4k$ vertices and $2^{n/4} = (2^{1/4})^n$ maximal flows.

Answer 2

Let $N$ be a network with nodes named $1,2,3,\dots,n$ and with an arc, of capacity one, from node $a$ to node $b$ precisely when $a<b$. Then node $1$ is the source, node $n$ is the sink, every flow is maximal, and the number of flows is $2^{n-2}$, because every subset of $\{\,2,3,\dots,n-1\,\}$ corresponds to a flow.