3

$|-2x|> \frac{-x}{2} -3$

This inequality isn't from a textbook, I made it out because I felt like there must be some cases when the methods I learnt in class won't work.

These are the methods I used and that I only know:

First method

  1. $-2x>\frac{-x}{2}-3$→ $x<2$
  2. $-(-2x)>\frac{-x}{2}-3$→ $x>-1.2$

Answer: $-1.2<x<2$

And after checking by substituting any number smaller than $2$ or bigger than $-1.2$, I get correct answers.

Second method

  1. $(|-2x|)^2 > (\frac{-x}{2}-3)^2$

Answer: $-1.2<x<2$

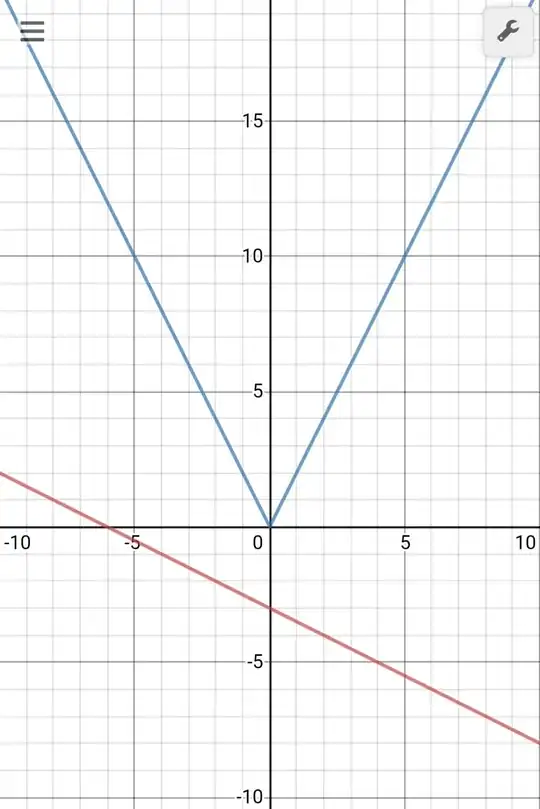
But this answer is wrong because looking at the graph I can see that the absolute value function is always above the straight line.

The answers I get are true if the straight line had an absolute value sign too or because of the parts under the x-axis of functions $-2x$ and $-(-2x)$ that no longer exist because of the absolute value sign.

So how can I solve this inequality without drawing? And how does I know that the answers I get are wrong or incomplete when solving anything similar?

Manar
  • 371

4 Answers4

2

$|-x|$ is the same as $|x|$. $$|2x| \gt -\frac x2 -3 $$ For $x\gt -6$, this will hold as the RHS is $\le 0$ (and also the LHS is not zero when the RHS is zero). For $x\le-6$, it is equivalent to $$-2x \gt -\frac x2-3 \implies \frac{3x}{2}\lt 3 \implies x\lt 2$$ which is always true in this case. Hence, all real numbers are solutions.

Vishu
  • 14,469
2

Here is how I would solve this problem: $$ |-2x|=|2x|>-\frac{x}{2}-3 \, . $$ If $x\geq0$, then the inequality becomes $$ 2x>-\frac{x}{2}-3 \\ \frac{5}{2}x>-3 \\ x > -\frac{6}{5} \, . $$ However, it is only true that $2x>-\frac{x}{2}-3$ when $x\geq0$. Hence, not all of the solutions we have found are valid. We are left with $x\geq0$.

If $x<0$, the inequality becomes $$ -2x>-\frac{x}{2}-3 \\ 2x < \frac{x}{2}+3 \\ \frac{3}{2}x<3 \\ x<2 \, . $$ The condition that $x<0$ and $x<2$ is equivalent to the condition that $x<0$—if a number is smaller than $0$, it is certainly smaller than $2$. Putting the two solutions together, we find that this is true for all values of $x$. Because of the difficulty of splitting the problem up into different cases, I think it is easier to solve this equation graphically than algebraically.

Joe
  • 19,636
1

If $x\ge0$ then $|-2x|=2x$, and if $x<0$ then $|-2x|=-2x$.

So we have (1) $x\ge0$ and $2x>-\frac x2-3\iff x>-\frac65$

or (2) $x<0$ and $-2x>-\frac x2-3\iff x<2$,

which is equivalent to (1) $x\ge 0$ or (2) $x<0$, which is equivalent to $x\in\mathbb R$.

J. W. Tanner
  • 60,406
  • I know this method! We used it once in class but with equations never with inequalities. But I was wondering about how I can decide whether to use it or to use the other methods by looking at the problem. – Manar Dec 17 '20 at 19:54
  • 1
    This is like your first method but being more careful – J. W. Tanner Dec 17 '20 at 20:04
1

The fastest way for me is to recognize $f(x)=|-2x|+\frac x2 +3$ is piecewise linear, and the only turning point is $0$.

Now $f(-\infty)=+\infty, f(0)=3>0, f(+\infty)=+\infty$, therefore $f(x)>0,\forall x \in \mathbb R$.

For some other examples of this type, check here.

Neat Math
  • 4,790
  • Oh dude this is way beyond my level in math! I haven't studied the f(−∞) or the piecewise functions or ∀x so I don't think I can get it but thanks :D – Manar Dec 17 '20 at 20:03
  • You can just make a plot of $f(x)$ against $x$ and you'll see... – Neat Math Dec 17 '20 at 22:29