Integral containing exponential

Question

I am trying to prove below (Reference: Green's function with application, page 159): $$\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{e^{i(x-y)\tau}}{\tau^4-a^4}d\tau=\frac{1}{4a^3}(ie^{ia|x-y|}-e^{-a|x-y|})$$

When trying to calculate the integral, I used Wolfram, and I get the following: $$\int\frac{e^{(x-y)i\tau}}{\tau^4-a^4}d\tau=\frac{1}{4}\sum_{{\omega:a^4-\omega^4=0}}\frac{e^{i(x-y)\omega}Ei(iA(\tau-\omega))}{\omega^3}+const$$ I am not sure how to deal with Ei function for an imaginary number with specified integral boundary.

Answer 1

To calculate this integral use complex analysis. We make a contour with the real line and a semi-circle through the upper-half of the complex plane.

As the radius of the semi-circle goes to infinity, the integral along this piece of the contour goes to $0.$

Now we just need to examine the residuals.

$\tau^4 - a^4 = (\tau - a)(\tau - ia)(\tau + a)(\tau + ia)$

Two of these poles will be inside the contour, and 2 will be outside the contour. In order to know which two to pick, lets assume that a has positive real and imaginary parts.

$\oint_\gamma \frac {e^{i|x-y|\tau}}{\tau^4 - a^4} \ d\tau$

$2\pi i \left[\lim_\limits{\tau \to a} \frac {e^{|x-y|\tau}}{\tau^4 - a^4}(\tau - a) + \lim_\limits{\tau \to ia} \frac {e^{|x-y|\tau}}{\tau^4 - a^4}(\tau - ia)\right]$

$2\pi i \left[\frac {e^{i|x-y|a}}{4a^3} + \frac{e^{i|x-y|(ia)}}{4(ia)^3}\right]$

$2\pi i \left[\frac {e^{i|x-y|a}+ie^{-|x-y|a}}{4a^3}\right]$

$2\pi \left[\frac {ie^{i|x-y|a} - e^{-|x-y|a}}{4a^3}\right]$

Answer 2

@Doug M already posted an answer assuming that $a$ is neither real nor pure imaginary. In this answer, I will tackle the opposite case, i.e., the case with $a > 0$.

If $a > 0$, then the integrand suffers from poles $\pm a$ along the real line, and so, the integral does not converge in ordinary sense. For this reason, we will interpret the integral in Cauchy principal value sense. Then by noting that the imaginary part of the integrand is an odd function, we get

$$ I := \frac{1}{2\pi} \operatorname{PV}\! \int_{-\infty}^{\infty} \frac{e^{i(x-y)\tau}}{\tau^4-a^4} \, \mathrm{d}\tau = \frac{1}{2\pi} \operatorname{PV}\! \int_{-\infty}^{\infty} \frac{\cos((x-y)\tau)}{\tau^4-a^4} \, \mathrm{d}\tau. $$

In particular, the integral depends only on $k := \left| x - y \right|$.

Now by applying the residue theorem applied to the contour integral along the dented semicircular arc

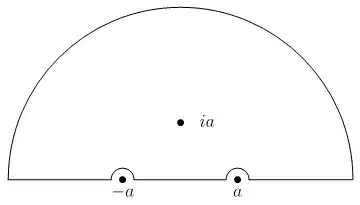
and then letting the outer radius to $\infty$ and the inner radii to $0^+$, we get

\begin{align*} I &= \frac{1}{2\pi} \operatorname{PV}\! \int_{-\infty}^{\infty} \frac{e^{ik\tau}}{\tau^4-a^4} \, \mathrm{d}\tau \\ &= \frac{1}{2\pi} \biggl( i\pi \, \mathop{\operatorname{Res}}_{z=a} \, \frac{e^{ikz}}{z^4-a^4} + i\pi \, \mathop{\operatorname{Res}}_{z=-a} \, \frac{e^{ikz}}{z^4-a^4} + 2i\pi \, \mathop{\operatorname{Res}}_{z=ia} \, \frac{e^{ikz}}{z^4-a^4} \biggr) \\ &= \frac{i}{2} \frac{e^{ika}}{4a^3} + \frac{i}{2} \frac{e^{-ika}}{4(-a)^3} + i \frac{e^{-ak}}{4(ia)^3} \\ &= - \frac{1}{4a^3}\bigl( \sin(ak) + e^{-ak} \bigr) \\ &= - \frac{1}{4a^3}\bigl( \sin(a\left|x-y\right|) + e^{-a\left|x-y\right|} \bigr). \end{align*}

Notice that this coincides with the real part of the proposed answer by OP.