Supremum of $\int_{-\infty}^{\infty}\frac{p'(x)^2}{p(x)^2+p'(x)^2}\,\mathrm{d}x$

Question

Question. Let $P_d = \{ p \in \mathbb{R}[x] : \deg p = d\}$ denote the set of all degree $d$ polynomials with real coefficients. Also, for $p \in \mathbb{R}[x]$, define

$$ I(p) = \frac{1}{\pi} \int_{-\infty}^{\infty}\frac{p'(x)^2}{p(x)^2+p'(x)^2}\,\mathrm{d}x. $$

Is it possible to identify the supremum of $I(\cdot)$ over $P_d$? In other words, what is

$$ C_d := \sup_{p \in P_d} I(p) = \ ? $$

This question is motivated by this posting. Here are some observations:

1. If $p \in P_d$ has only real zeros, then $I(p) = d$ holds. (See this and this.)

2. $I(p) \leq d^{3/2}$ for any $p \in P_d$. Indeed, write $p(x) = a (x - \alpha_1) \dots (x - \alpha_d)$. Then by the Cauchy-Schwarz inequality, $$ \left| \frac{p'(x)}{p(x)} \right|^2 = \left| \sum_{k=1}^{d} \frac{1}{x - \alpha_k} \right|^2 \leq d \sum_{k=1}^{d} \frac{1}{\left| x - \alpha_k \right|^2}. $$ Now by noting that the map $f(t) = \frac{t}{t+1}$ is increasing and subadditive for $t \geq 0$, \begin{align*} I(p) &= \frac{1}{\pi} \int_{-\infty}^{\infty} f\biggl( \left| \frac{p'(x)}{p(x)} \right|^2 \biggr) \, \mathrm{d}x \\ &\leq \sum_{k=1}^{d} \frac{1}{\pi} \int_{-\infty}^{\infty} f\biggl( \frac{d}{\left| x - \alpha_k \right|^2} \biggr) \,\mathrm{d}x \\ &\leq \sum_{k=1}^{d} \frac{1}{\pi} \int_{-\infty}^{\infty} f\biggl( \frac{d}{(x - \operatorname{Re}(\alpha_k))^2} \biggr) \,\mathrm{d}x \\ &= d^{3/2}. \end{align*} In particular, we learn that $d \leq C_d \leq d^{3/2}$.

3. When $d = 2$, we can show that $C_2 = 2$ by using the first part and a direct computation.

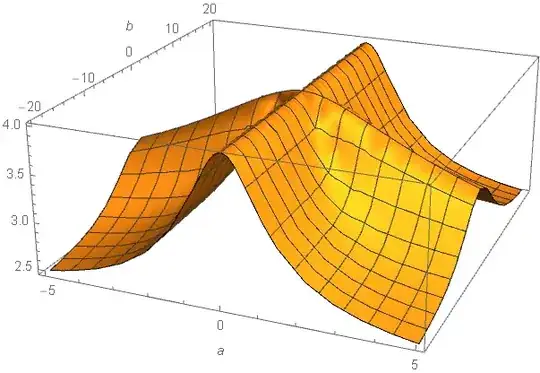
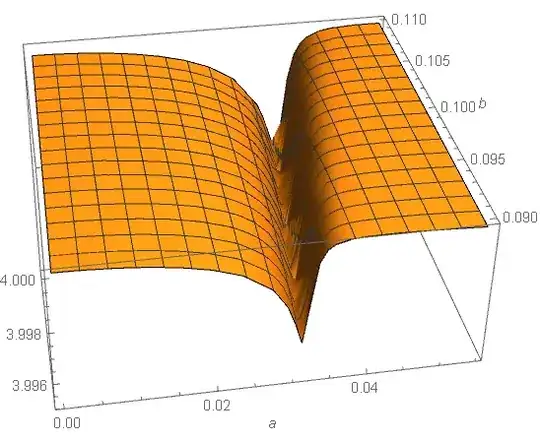
4. For $d \geq 4$, we seem to have $C_d > d$. Indeed, numerical experiments reveal that we can find $a, b > 0$ satisfying $$I((x^2+a^2)(x - b)^{d-2}) > d.$$ However, $C_d$ seems much smaller than $d^{3/2}$, differing from $d$ only by a tiny fraction.

5. A simple computation shows that $$ I(p) = d - 2 \sum_{\substack{\alpha : \operatorname{Im}(\alpha) < 0 \\ p(\alpha) = ip'(\alpha) }} \operatorname{Re} \biggl( \frac{1}{1+p''(\alpha)/p(\alpha)} \biggr). $$ This provides an alternative proof of part 1. Indeed, if $p$ has only real zeros, then $\operatorname{Im}\bigl(\frac{p'(z)}{p(z)}\bigr)$ and $\operatorname{Im}(z)$ always have the opposite signs, and so, the summation part in the above formula vanishes.

Answer 1

For point $4)$, what numerical simulation did you use? I tried to simulate that specific polynomial, $p(x)=(x^2+a^2)(x-b)^2$, for $d=4$ and I got

for $I(p)$. Indeed for $a=0$, $p(x)$ has all real roots so by your point $1)$ the center line in the above graph is exactly $4$. Since it appears that everything is increasing towards this line, it would appear that the maximum of $I(p)$ is $4$ for this case.

---

EDIT:

After getting the points $a=\frac{1}{\sqrt{500}}$ and $b=\frac{1}{10}$ I can recreate the same plot above but zoomed in:

The right side of this graph is just ever so slightly greater than $4$. However, this graph just raises more questions than answers in my mind: what is that valley, why is it so steep and sudden, etc.?