I'm trying to automate creation of a curve in PowerPoint.
Here's an image of what I'm working towards:
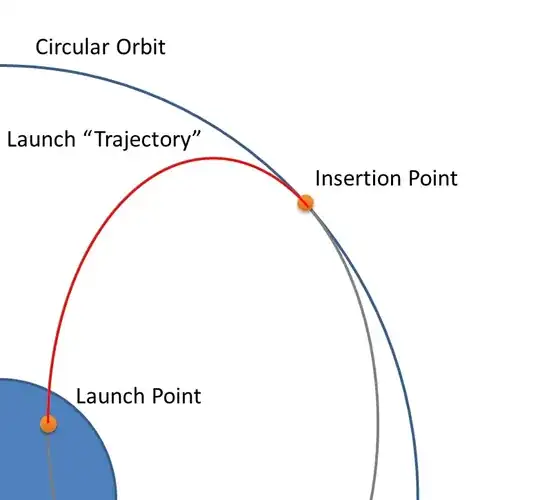
I'm trying to show a diagram of a rocket trajectory from a launch site on Earth to a circular orbit. The math that I can't figure out is how to solve for an ellipse that connects the launch point (x1, y1) to the orbit insertion point (x2, y2) and is tangent to a vertical line at the launch point and tangent to the circular orbit. My approach has been to use (x-h)^2/a^2 + y^2 / b^2 = 1 because while I can set the horizontal axis of the ellipse at y=0, I don't know where the x coordinate of the center might fall, so I have an x-offset, h. I found an equation for the slope of a tangent line to an ellipse at a point as m = a^2*x/(b^2*y). I'm not sure if this is the right equation because sometimes the desired ellipse is longer horizontally and sometimes it might be longer vertically. If my insertion point is 45 degrees along the 1st quadrant of the orbit, then the tangent line has a slope of m = -1. Substituting the coordinates of the insertion point in to the slope equation, I can establish a relationship between a and b. Then I solved the ellipse equation for h as a function of x, y, and a (substituting for b with the slope relationship). Then I got 2 "h" equations by substituting the launch point, (x1, y1) and the insertion point, (x2, y2). Then I iterated to find an "a" value that minimized the difference between the 2 "h" equations. This successfully generated an ellipse that intersected the two points, but I think the slope at the insertion point is wrong (doesn't match the orbit), and it only appears to work for ellipses that are longer horizontally.
I apologize for this terribly formatted question. I've spent all day at work trying to figure this out and I'm stumped. Many of the solutions to similar problems online a just out of reach for me to understand how to apply it to my situation.
Thanks for any help anyone might can provide.
[edit] Using a modification of alex.jordan's method I solved my problem. Here's my work: https://www.dropbox.com/s/61mmyuz4hmh2ry9/ellipses.pdf
And here's some Matlab code showing an application of the method and plotting a demonstration of the solution:
figure('Name','Ellipse Tangent to Orbit', ...
'Color',[1,1,1],'NumberTitle','off', ...
'Units','Normalized', 'Position',[0.1,0.1,0.8,0.8], ...
'Visible','on');
axes;
hold on;
earthX = 0;
earthY = 0;
plot(earthX,earthY,'bo');
r = 700;
theta = 45 * pi/180;
%Insertion Point
s = earthX + r * cos(theta);
t = earthY + r * sin(theta);
%orbit
theta_mat = linspace(0,pi/2,100);
x_orbit = earthX + r*cos(theta_mat);
y_orbit = earthY + r*sin(theta_mat);
plot(x_orbit, y_orbit,'b--')
%launch point
x0 = 50;
y0 = 100;
plot(x0,y0,'ro');
plot(s,t,'ro');
%Slope at tangency point
m = -s/t;
%Vertical offset of ellipse equals coordinate of launch point
k = y0;
%b polynomial
% b^2 term
a0 = 2*t^3*x0*s^3*(t-k)^3-2*t^3*s^4*(t-k)^3-t^4*s^2*(t-k)^4;
% b term
a1 = 0;
% constant term
a2 = t^2*x0^2*s^4*(t-k)^4-2*t^2*x0*s^5*(t-k)^4-2*t^3*x0*s^3*(t-k)^5 + ...
t^2*s^6*(t-k)^4+2*t^3*s^4*(t-k)^5+t^4*s^2*(t-k)^6;
%b = max(roots([a0,a1,a2]));
%Solving for b (reduced quadratic formula)
b = abs(sqrt(-a0*a2)/a0);
%Solve for a
a = sqrt((b^4*t^2-b^2*t^2*(t-k)^2)/(s^2*(t-k)^2));
%Solve for h
h = s-a^2*s*(t-k)/(b^2*t);
% X values for ellipse
x = linspace(h-a,h+a,100);
%y values for ellipse
y = b/a*sqrt(a^2-(x-h).^2)+k;
plot(x,y,'b-')
axis square
Finally here's the plot:
https://www.dropbox.com/s/71t4tuw3bqv0xr1/orbits_verified.png