Let $$ M_1=\left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \\ \end{array} \right), \qquad M_2=\left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \end{array} \right),\qquad v = \left( \begin{array}{c} 1 \\ 1 \\ \end{array} \right) $$
and consider the $n$-fold random product, for $n \in \mathbb N$. More precisely, let
$$\Psi_n := \log \| M_{i_1}M_{i_2}\cdots M_{i_n}v \|_{L^1}:$$ where each $i_k$ are i.i.d., equal to 1 or 2 with equal probability.
Scaling by $2^{-n}$, in this question we consider $\Phi_n$ as a compactly supported probability measure on $\mathbb R$ (i.e. a weighted sum of Dirac deltas).
Central Limit Theorem
For probability measures $\mu_n, \mu$, we here say
$$\mu_n\stackrel{\text{dist.}}\longrightarrow \mu$$
if, for each $-∞ < a \leq b < ∞$,
$$\mu_n\big([a,b]\big) \to \mu([a,b]) .$$
Under certain hypotheses on the $M_i$, one would see, for generic $v$, that $\Psi_n$ satisfies a kind of Central Limit Theorem:
I.e., that there exist constants $\lambda_\ast > 0$ and $\sigma >0$ such that
$$ \frac{\Psi_n - n \lambda_\ast}{\sigma^2\sqrt n} \stackrel{\text{dist.}}\longrightarrow N(0,1) \qquad\text{as }n \to ∞,$$
where $N(0,1)$ is the standard normal distribution.
Reality
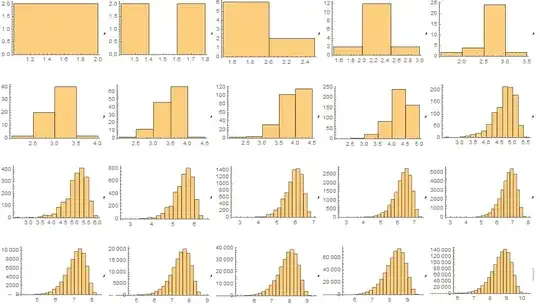
Calculating some histograms in Mathematica, the shape of $\Psi_n$ seems to not be converging to a Gaussian, but to some kind of skewed distribution: see pictures below.
Questions:
- What can $\Phi_n$ be converging to, if anything?
- How would one prove that $\Phi_n$ is not converging to a Gaussian?