The second part is a separate proof from Helly's theorem. It looks like Dave wrote this proof out first, then later realized Helly's theorem was applicable at the indicated point and added the edit.
For his own idea, Dave needs a pair of lines that are not parallel to each other. But of course, this isn't guaranteed, so he breaks the proof into two cases: Either
- All $n$ lines are parallel to each other, or
- There are at least two lines that intersect.
Then he examines the first case: If all the lines are parallel, then they have to be in order, with two outside lines and all the others inbetween. If you take the two outside lines and pick any of the middle lines (this is where the proof fails for the $n = 2$ case, as mentioned in the comments), then you have a triple of lines, and per the hypothesis, there is some circle intersecting all three. But the only way the circle can intersect both outside lines is to pass through all the lines in the middle. So it intersects every line. The parallel case is proved.
Next he proves the second case: Two of the lines $\ell_1$ and $\ell_2$ intersect. The cylinders of radius $1$ about them, $C_1$ and $C_2$ therefore intersect to form a parallelogram (actually, a rhombus). This is a closed polygon. Number the cylinders about the remaining lines as $3$ and on in some arbitrary order.
Now we note a couple things about the Sets $P_k = \bigcap_{i=1}^k C_i$, for any $k \ge 2$. Because the intersection of convex sets is also convex, each $P_k$ is convex. Further, if $P_{k-1}$ is a polygon and $P_k \ne \varnothing$, then $P_k = C_k \cap P_{k-1}$ is also a polygon. This is because the intersection just cuts off from $P_{k-1}$ the portions that extend beyond $C_k$'s two boundary lines. And since $P_2$ is a polygon, by induction, so are all the $P_k$ for $k > 2$.
Now suppose that $\bigcap_{k=1}^n C_k = \varnothing$. Then there has to be some largest $p < n$ such that $P_p = \bigcap_{k=1}^p C_k \ne \varnothing$. Now since $p$ is the largest possible, $P_p\cap C_{p+1} = \varnothing$, and in particular $P_p$ does not intersect the line $\ell_{p+1}$. Dave uses an optimization argument to prove the intuitively obvious fact that the closest point of the solid polygon $P_p$ to $\ell_{p+1}$ will be some vertex $v$ of $P_p$. Label the two boundary segments meeting at $v$ by $b_i$ and $b_j$. Because of how the polygon $P_p$ is formed, these segments are parts of the boundaries of two cylinders $C_i, C_j$ for some $i, j \le p$. Now $b_i$ and $b_j$ are at best parallel to $\ell_{p+1}$, or else they slant away from $\ell_{p+1}$ as you move away from $v$. Otherwise $v$ would not be the closest point of $P_p$ to $\ell_{p+1}$.
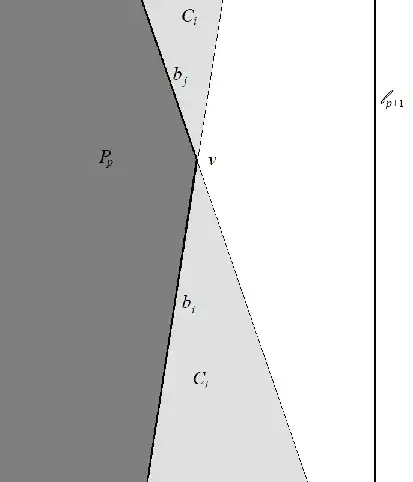
But the intersection $C_i\cap C_j$ is a rhombus lying on the same side of $b_i$ and $b_j$ as its subset $P_p$. Which means that $v$ is also the closest point of $C_i\cap C_j$ to $\ell_{p+1}$. But $v \notin C_{p+1}$, so it is a distance of more than $1$ away from $\ell_{p+1}$. Thus the same must be true of every point of $C_i\cap C_j$ to $\ell_{p+1}$. In particular, $C_i\cap C_j \cap C_{p+1} = \varnothing$, which means there can be no circle intersecting all three of $\ell_i, \ell_j, \ell_{p+1}$, a contradiction.
