Well, Wolfram Alpha says no. Why?
1 Answers
$$\sqrt[3]{-3} = -\sqrt[3]{3} \iff (\sqrt[3]{-3})^3 = (-1)^3(\sqrt[3]{3})^3 \iff -3=(-1)3 \iff -3=-3$$ So I would say it is true if we are talking about real numbers.
In fact in "Analisi Matematica" of Paolo Maurizio Sardi (CIttàStudi edizioni), we define roots in the following manner.
Theorem 1.7.1 Given an integer $n \ge 1$, and a real number $\alpha >0$, there exists one, and only one, real number $\beta>0$ such that $$\beta^n=\alpha \mbox.$$
Definition 1.7.3 The number $\beta >0$ found in the Theorem above is called $n$-th root of $\alpha$ and is denoted by $$\beta = \sqrt[n]\alpha \mbox.$$
Observation: $(\sqrt[n]\alpha )^m =\sqrt[n]{\alpha^m}$
Definition 1.7.4 Let $m\in \mathbb{Z}$, let $n\ge 1$ be an integer and let $\alpha >0$. We set $$\alpha^{m/n}=(\sqrt[n]\alpha )^m $$
Observation: we now want to define all of this for negative real numbers. Let $-a<0$ and let $n \ge 1$ be an integer:
(1) if $n=2k$ is even, it is clear that there does not exists $\beta\in \mathbb{R}$ such that $$\beta^{2k}=(\beta^2)^k=-\alpha \mbox,$$ so we cant' do this in the reals;
(2)if $n=2k+1$ is odd and let $\beta >0$ be such that $\beta^{2k+1}=\alpha$ ($>0$), then $$(-\beta)^{2k+1}=-\alpha$$ so $-\beta$ is called the $n$-th root of $-\alpha$ an is denoted by $$-\beta=\sqrt[n]{-\alpha} \mbox.$$
You could then continue with defining roots with real exponent (going back to $a>0$), showing that the following definition is well-defined:
Definition 1.7.5:
(1) if $\alpha \ge 1$ and $\beta >0$ we set $$\alpha^{\beta}:= \sup\biggl{\{} \alpha^{m/n}:\frac{m}{n} \le \beta \biggr{\}}$$
(2) if $0<\alpha < 1$ and $\beta >0$ we set $$\alpha^{\beta}:=\frac{1}{(1/\alpha)^{\beta}}$$
(3) if $\alpha >0$ and $\beta >0$ we set $$\alpha^{-\beta}=\frac{1}{\alpha^{\beta}$$
(4) $\alpha^0=1$
(defined for every $\alpha>0$ and $\beta$ reals).
- 1,310
-
1But do we talk about real numbers when we have cube roots? For example third roots of unity? I am not sure. – Dietrich Burde Dec 03 '20 at 12:55
-
1
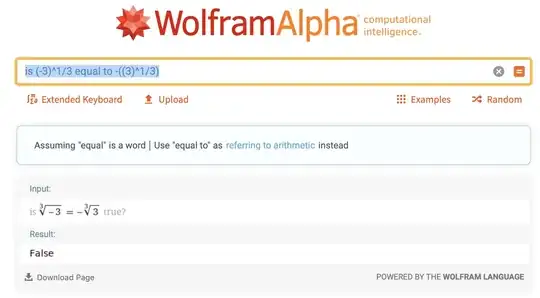
Cbrt(...). Sure enough, you can see that $ \sqrt[3]{-3} = -\sqrt[3]{3} $ – talbi Dec 03 '20 at 16:50