Convexity of the set with the fixed norm

Asked Dec 03 '20 at 10:30

Active Dec 03 '20 at 10:35

Viewed 49 times

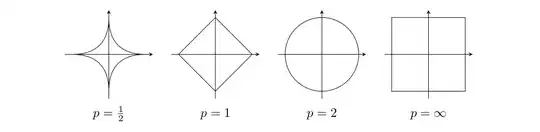
These are the circles $\Vert x \Vert = a, a > 0$ for various norms of the form $ \Vert x \Vert = \left(\sum_i |x_i|^p \right)^{1/p} $

And the $p = 1/2$ norm is not a norm, because it does not satisfy the triangle inequality : $$ \Vert x + y \Vert \leq \Vert x \Vert + \Vert y \Vert $$ And the set, with the fixed norm is not convex, whereas for other cases it is.

Does it hold for any norm, that the level set with the fixed norm is convex in order to satisfy the triangle inequality?

asked Dec 03 '20 at 10:30

spiridon_the_sun_rotator

Yes. You can prove that it is equivalent in the definition of a norm to ask that the triangle inequality is satisfied, or to ask that the unit ball is convex. – TheSilverDoe Dec 03 '20 at 10:36
@JoséCarlosSantos If I understand the question well, the OP asks if the convexity of the balls is equivalent to the triangle inequality. The answer is yes, but your link gives only one implication. – TheSilverDoe Dec 03 '20 at 10:38
1

@TheSilverDoe Then this question will have the rest of the answer. – José Carlos Santos Dec 03 '20 at 10:40
@JoséCarlosSantos Indeed, thank you :) – TheSilverDoe Dec 03 '20 at 10:44
@JoséCarlosSantos thanks for the links! – spiridon_the_sun_rotator Dec 03 '20 at 10:47

Convexity of the set with the fixed norm

0 Answers0