0

To visualize this, I've created the following diagram.
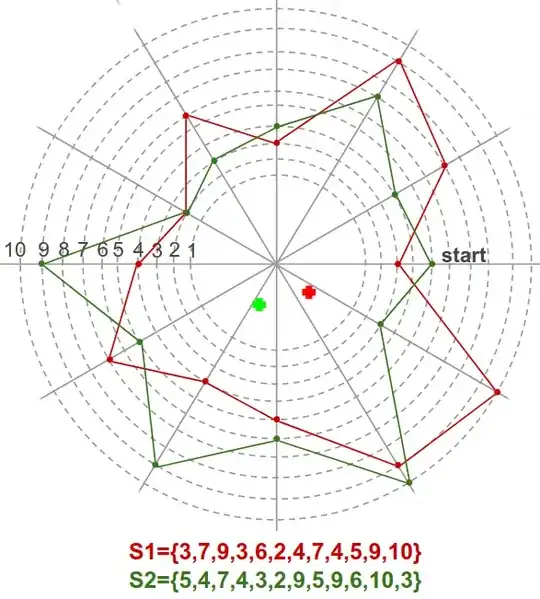
enter image description here
I have sets of 80 numbers each. Here, just to draw it easily, I'm showing them as sets of 12 numbers each. The sets S1 and S2. Each set can contain 12 numbers ranging from 1 to 10, and the order of the number in the set matters. i.e. {1,2,3} is not the same as {1,3,2}.
In 2D space, there are 10 concentric circles as shown by the dotted lines in the image. Each circle represents the possible values that can be contained in a set. Each of the straight lines jutting out of the center of the image, represents the position of each number in the set, starting from the "start" line. So since S1 has 3 as the first number, the first red dot is placed on the third concentric circle at the start line. Moving counter-clockwise, the next number is 7, which gets placed on the next line at circle 7 and so on.
Circles placed as such, form the red and green polygons shown in the image.

Question:
I want to find a unique center point for each such polygon formed by any such set containing 12 numbers where the numbers may be generated randomly. I've placed a red and green plus point for what I'd assume might be the approximate centers of the polygons.

  • I'm not particular about whether only the vertices of the polygon are considered for finding the center or whether the sides of the polygon are also considered.
  • I'm also not particular about whether the center point lies within
    the polygon or not.

I just want to ensure that each unique polygon should definitely have a unique center point on the given 2D space. Is there a formula to calculate it and is it possible to ensure a unique point? Do remember that I'll eventually be using sets of 80 numbers each, containing numbers ranging from 1 to 10.
I've seen the centroid formulae and this, but I'm not sure if they'd mathematically ensure unique center points.

Nav
  • 368
  • 1
    Do you mean unique center among all the polygons? If so, then that is not guaranteed. Many different symmetric polygons will all have a centroid at the origin, for example. – Andy Walls Dec 02 '20 at 13:19
  • That's why I'm stressing on "unique". If not a centroid, then some other formula that could give me a unique point. – Nav Dec 02 '20 at 14:36
  • So this sounds isomorphic to creating a cryptographic hash. Reduce N bytes down to M < N bytes and generate a number not likely to collide with another answer. Here you want to reduce 80 coordinates down to 1 coordinate and you want 0 collisions. I'm thinking there's an information theory answer as to why that's impossible. – Andy Walls Dec 02 '20 at 16:13

1 Answers1

1

For simplicity, I would use the centroid of a finite number of points, which is simply calculating the arithmetic mean of each coordinate. This is as if you have an equal weight at each of the points, and then find the balancing point. This is simple to implement without errors.

The other formulations you link to assume the weight is uniformly distributed across the whole area of the polygon. That will (if implemented correctly, and if given the vertices in order around the polygon) also give a uniquely determined centroid, but is slightly different to the above, and I see no reason why it would be preferred over the simpler one.

Note that as pointed out in the comments, there will always be distinct polygons that have the same centroid. There will be many that have the centroid in the origin (e.g. any polygon with rotational symmetry). There are also ones with matching centroids that are not in the origin, but those will be much rarer. However, given that you are using 80-gons, each vertex with 10 possible values, the probability of getting matching centroids is very small.

Jaap Scherphuis
  • 13,660
  • It does not have to be a centroid. Any formula that can give me a unique x,y point would do, as long as I get the same unique point when I supply the same vertices to the function. – Nav Dec 02 '20 at 14:39
  • @Nav If all 80 numbers are the same, you would probably expect the representative point to be in the centre. This means that the case with all values 1 and the case with all values 2 will have the same representative point. The only way to avoid that is to break the symmetry and not have any representative point be in the origin, regardless of symmetry. You could for example use a weighted average of the 80 points, where the weights are not all the same. If you use weights that have various irrational values, you can ensure that the representative points will always be unique. – Jaap Scherphuis Dec 02 '20 at 14:49
  • That's a nice idea! The comment from Andy (above) says it's something like a hash function, but the idea of using weights is cool. I'm not able to visualize how to use irrational values to achieve this though. – Nav Dec 02 '20 at 17:11
  • @Nav You could let the weights be $\sqrt{p_i}$ where the $p_i$ are 80 different prime numbers. If those weights vary too much in size you can scale them by a rational factor. For example, you can use $\frac{100}{174}\sqrt{3}$, $\frac{100}{264}\sqrt{7}$, $\frac{100}{331}\sqrt{11}$, and so on. These square roots are linearly independent over the rationals, so the resulting combinations are always unique. Best to avoid using $\sqrt{2}$ and $\sqrt{5}$ in the weights because the sine and cosine of the angles involved with $80$ points will contain those two roots already. – Jaap Scherphuis Dec 02 '20 at 17:30
  • Your suggestion led me to this: http://www.fractalcurves.com/Root4Square.html and this: https://math.stackexchange.com/questions/3003672/convert-infinite-2d-plane-integer-coords-to-1d-number and the Morton code: https://stackoverflow.com/questions/30990301/what-is-this-algorithm-mapping-coordinates-to-numbers-called. Meanwhile, I also got an idea of using a kind of an attractant force to generate a unique pattern. Will try some of these. Thank you very much for your help. – Nav Dec 07 '20 at 14:00