4

I was thinking about the following problem:

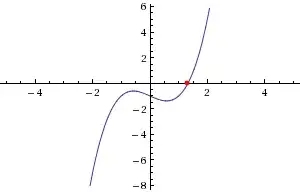
Let $f(u)=u^3-u-1$. Then I have to verify whether the following statements are true/false?

1.Starting with the initial guess $u^{(0)}=1.5,$ the fixed point iterates of the equation $u=g(u)$,where $g(u)=u^3-1$ converges

2.If $u^{\star}$ is a root of the equation $f(u)=0$ and $u^{\star} >1,$ then $u^{\star} $ is a stable fixed point of the equation $u=g(u)$

3.$f(u)=0$ has a root between $1$ and $2$

4.Staring with the initial guess $u^{(0)}=1.5,$ the fixed point iterates of the equation $u=\tilde{g}(u),\text{where} \space \tilde{g}(u)=\sqrt{1+u^3} $ converge.

Here,option 3 is true as we see that $f(1)<0 \space \text{whereas} f(2)>0$ .But I am not sure about the other options .How can I check other options?

Can someone point me in the right direction?

Thanks in advance for your time.

Community
  • 1

2 Answers2

3

Hints

  • There is a root at: $u = 1.3247179572447460260$ and the other two roots are imaginary.

Part 1.

Here are the iterates. What do you notice is happening from iterate to iterate?

  • $u_1 = 2.375$
  • $u_2 = 12.396484375$
  • $u_3 = 1904.00277223$
  • $u_4 = 6902441412.84$
  • $u_5 = 3.28857830393E+29$
  • $u_6 = 54608.3924665$
  • $\ldots$
  • $u_{40} = 5153.0115226$

So, what can you say about convergence?

Part 2

You just need to think about this one a bit (go back and look at the FP theory.

Part 3

Correct. We could have also plotted the function to see:

enter image description here

Part 4

  • $u_1 = 2.09165006634$
  • $u_2 = 3.18605854313$
  • $u_3 = 5.77421697131$
  • $u_4 = 13.9112014761$
  • $u_5 = 51.8952497366$
  • $u_6 = 373.846193564$
  • $\ldots$
  • $u_{40} = 1.5659769437E+15$

So, what can you say about convergence?

Amzoti
  • 56,093
0

There is a condition you must check to verify that the $g(x)$ you've chosen converge:

$$|g'(u)| \leq \lambda <1$$

As for the suggested $g(x)$, apparently both of them diverge.

Gigili
  • 5,503
  • 8
  • 41
  • 62