4

Evaluate: $$ \int \frac{x^2}{\sqrt{1-x^2}}\,dx$$

The solution I came across does a $u$-substitution by letting $x = \sin(t)$. But why $\sin(t)$? It seems a lot like guessing to me - should I just guess the right $x$ for substitution? Why not $\cos(t)$? Is there any way that I could identify that "this" expression is solved by "that" trig substitution?

DMcMor
  • 9,407
bgly
  • 311
  • 1
    You can try $x = \cos t$, and that should still lead to the same answer. – peterwhy Dec 01 '20 at 20:56
  • 2
    $x=\cos(t)$ is a perfectly acceptable substitution (you can still leverage the identity $\cos^2(t)+\sin^2(t)=1$), but $x=\sin(t)$ is usually preferred because its derivative doesn't have any negative signs mucking it up. – Alann Rosas Dec 01 '20 at 21:01
  • 2
    There is nothing wrong with guessing. At worst, the guessed substitution will not help solve the problem. – Somos Dec 01 '20 at 21:10
  • Unlike differentiation, integration is genuinely hard: sometimes we have to have some creative insight or even guess, to see the solution. Here's a passage on this which I quite like (here, page 2): "Consider ... a famous joke by the comedian Steve Martin: 'You can be a millionaire and never pay taxes ... First, get a million dollars. Then when they ask you why didn't you pay taxes say "I forgot" and when they say "You forgot!?" say "say "Well excuuuuuuuuuuse me."' The Steve Martin solution to the [antiderivative] problem might go something like this: – Noah Schweber Dec 01 '20 at 21:47
  • First, get the right function. Then, show it has the derivative you were searching for. Now try to ignore the fact that this 'Martin integral' is probably the most powerful method of integration known and, in practice, has successfully computed more antiderivatives than all other solutions combined. Consider instead how hard it is to "guess" the antiderivative." – Noah Schweber Dec 01 '20 at 21:48

2 Answers2

4

Draw a triangle! When looking at the term $\sqrt{1 - x^{2}}$ in the integrand, you should immediately be reminded of the Pythagorean Theorem. If you draw a right triangle with hypotenuse length $1$, and side lengths $x$ and $\sqrt{1 - x^{2}}$, you end up with the following triangle. I've labelled the remaining two angles $s$ and $t$. So, if you want to isolate $x$ for a potential change of variables, based on the triangle, you can either use $\sin(s) = x$ or $\cos(t) = x$. Either would give you a valid change of variables.

enter image description here

DMcMor
  • 9,407
2

I think that the OP's question refers to how to distinguish why to make this change of variable. Now, I will write the answer to that question.

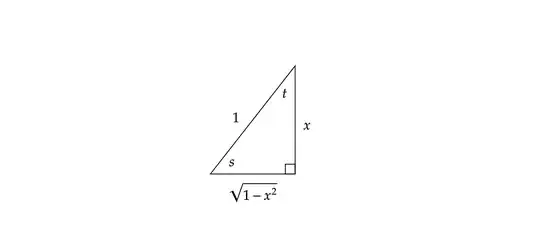
Suppose you want to solve an integral of the form $$\color{blue}{\boxed{\int R(x,\sqrt{a^{2}-x^{2}})dx}}$$ As in your problem, that you have $$\color{red}{\text{Example:} \quad \int \frac{x^{2}}{\sqrt{1^{2}-x^{2}}}dx}$$So, this integral becomes a trigonometric integral with the change of variable $$\color{green}{\boxed{x=a\cos(t)}} \quad \color{green}{\boxed{x=a\sin(t)}}$$ As the MathS users indicate in the comments. Also note that you can also perform the variable change $$\color{green}{\boxed{x=a\tanh(t)}}$$ and this variable change transforms the integral into a hyperbolic integer.