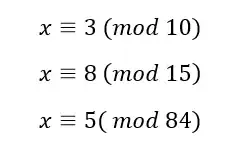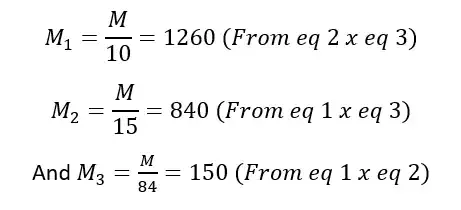Chinese Remainder Theorem, what to do when no inverse?

Question

I have the three equations:

Using the Chinese Remainder Theorem I have found that 10.15.84 are coprime, however they are not pairwise co-prime.

I have worked out the following:

However, none of these values have multiplicative inverses. Where do I go from here?

Can you solve $x\equiv3\pmod5, x\equiv2\pmod3, x\equiv5\pmod7, x\equiv1\pmod4$? — J. W. Tanner, Nov 30 '20 at 22:33
Solved with the 4 equations to get x=173. Please can you explain how you split up the equations in this way? — anon12352432, Nov 30 '20 at 22:37
See this post for solving CRT problems when the moduli are not pairwise coprime. — Arturo Magidin, Nov 30 '20 at 23:45
Please do not use images; they are not searchable, and they may be non-accessible to people using screen readers. Use MathJax to typeset mathematics. Here’s a tutorial — Arturo Magidin, Nov 30 '20 at 23:47

score 1 · Answer 1 · edited Nov 30 '20 at 23:46

1

I prefer to separate the system into the prime power factors in the first place.

$$x\equiv 3\pmod{10}\iff x\equiv 1\pmod{2}\text{ and } x\equiv 3\pmod{5}$$

$$x\equiv 8\hspace{3pt}(mod\hspace{3pt} 15) \iff x\equiv 2\hspace{3pt} (mod\hspace{3pt} 3) \text{ and }x\equiv 3 \hspace{3pt}(mod\hspace{3pt} 5)$$

$$x\equiv 5\hspace{3pt}(mod\hspace{3pt} 84) \iff x\equiv 2\hspace{3pt} (mod\hspace{3pt} 3) \text{, }x\equiv 1 \hspace{3pt}(mod\hspace{3pt} 4)\text{ and }x\equiv 5 \hspace{3pt}(mod\hspace{3pt} 7)$$

So, your initial system is equivalent to:

$$x\equiv 1\hspace{3pt} (mod\hspace{3pt} 4)$$ $$x\equiv 2\hspace{3pt} (mod\hspace{3pt} 3)$$ $$x\equiv 3 \hspace{3pt}(mod\hspace{3pt} 5)$$ $$x\equiv 5 \hspace{3pt}(mod\hspace{3pt} 7)$$

edited Nov 30 '20 at 23:46

Arturo Magidin

398,050

answered Nov 30 '20 at 22:41

JPMarciano

1,075

1

I suppose you mean prime power factors – J. W. Tanner Nov 30 '20 at 22:45
1

Use \pmod to get the parenthetical modulo operation typeset and spaced out properly. See the edit on the first displayed equation. – Arturo Magidin Nov 30 '20 at 23:46

score 1 · Accepted Answer · answered Nov 30 '20 at 22:42

The Chinese remainder theorem works for pairwise co-prime moduli,

and, as you noted, yours are not pairwise co-prime. Now

$x\equiv3\bmod10\iff x\equiv1\bmod2$ and $x\equiv3\bmod5$,

$x\equiv8\bmod15\iff x\equiv2\bmod3$ and $x\equiv3\bmod5$, and

$x\equiv5\bmod84\iff x\equiv2\bmod3, x\equiv1\bmod4$ and $x\equiv5\bmod7$.

Putting this all together, your system is satisfied when

$x\equiv3\bmod5, x\equiv2\bmod3, x\equiv5\bmod7, $ and $x\equiv1\bmod4$,

which you solved (per comments) using CRT to get $x\equiv173\bmod420$.

Chinese Remainder Theorem, what to do when no inverse?

2 Answers2